Incorporating Hierarchy into Text Encoder: a Contrastive Learning Approach for Hierarchical Text Classification
ACL 2022,使用Graphormer与对比学习处理层次文本分类(HTC)。
Overview

- paper: https://arxiv.org/pdf/2203.03825.pdf
- code: https://github.com/wzh9969/contrastive-htc
- dataset: RCV1-V2 WOS NYT
Background
现有的HTC方法已经引入了各种层次信息,主要有两种方式。
- 将文本和标签分别编码,得到混合表示。
- 将层次信息融入编码器,得到层次感知的文本表示。
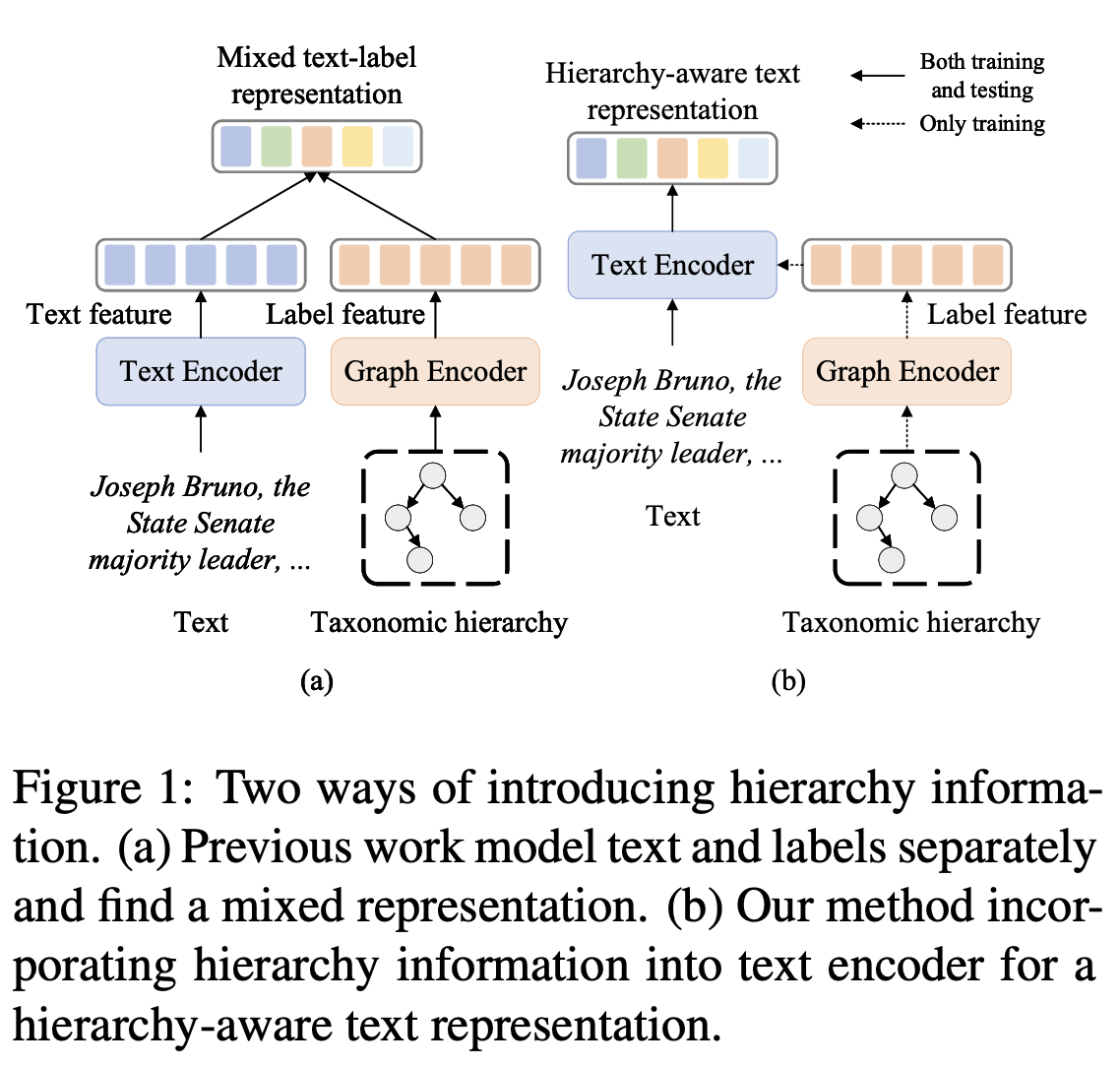
本文引入了对比学习以获得层次感知的表示,尝试构建高质量的正样本。现有的方法包括数据增强和对抗攻击等,这些要么是无监督要么是任务无关的。
作者的motivation主要是:文本分类时大多数的词或token其实并不重要,而少量的关键词对结果有很大的影响。给定文本序列及其标签,只保留少量关键词的短序列也应该保持同样的标签。因此,本文的idea和对抗攻击有点像,希望找出对分类影响最大的tokens,但对抗攻击是试图修改它们,而本文修改的是不重要的tokens。
Method
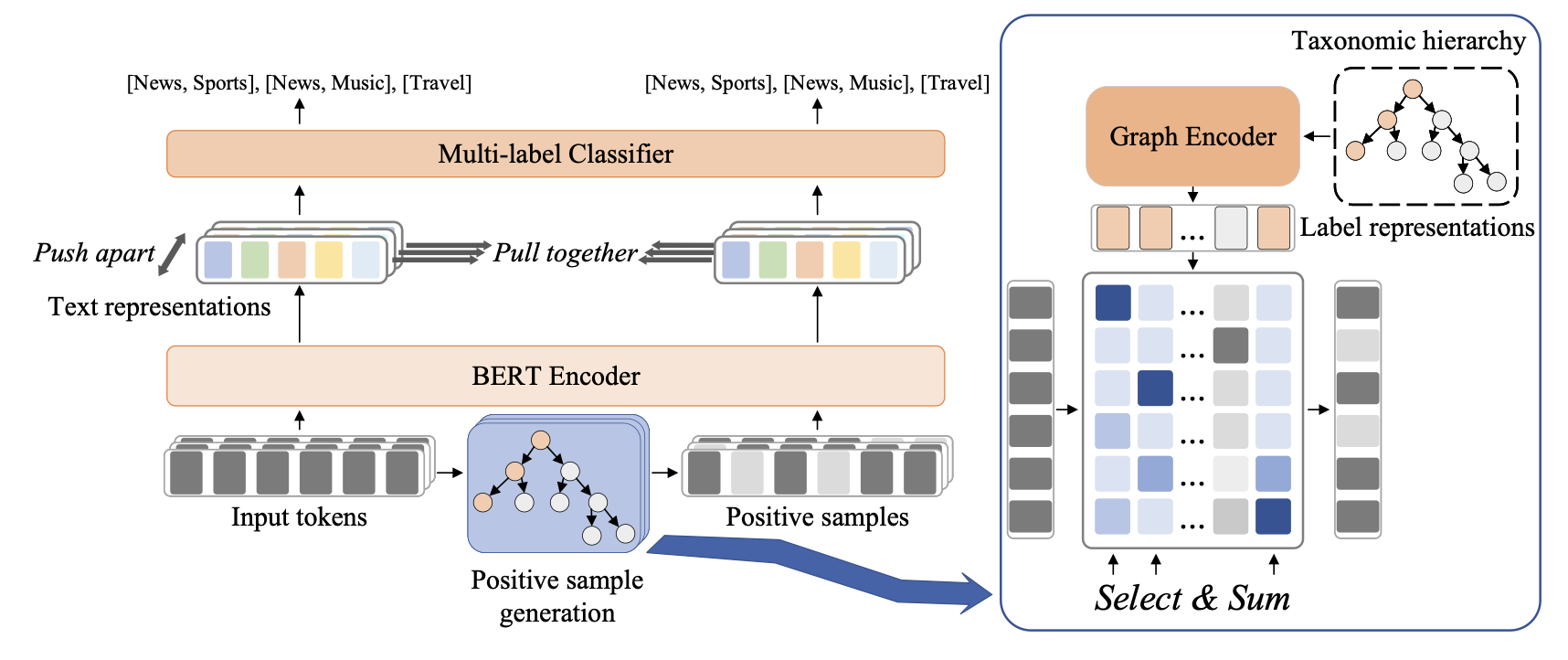
Text Encoder
文本嵌入采用BERT,老生常谈。 \[ x = \{[CLS], x_1, x_2, \cdots, x_{n-2}, [SEP]\} \] 文本表示\(H\in\mathbb{R}^{n\times d_h}\),采用\(h_x=h_{[CLS]}\)作为句子表示 \[ H = \mathrm{BERT}(x) \]
Graph Encoder
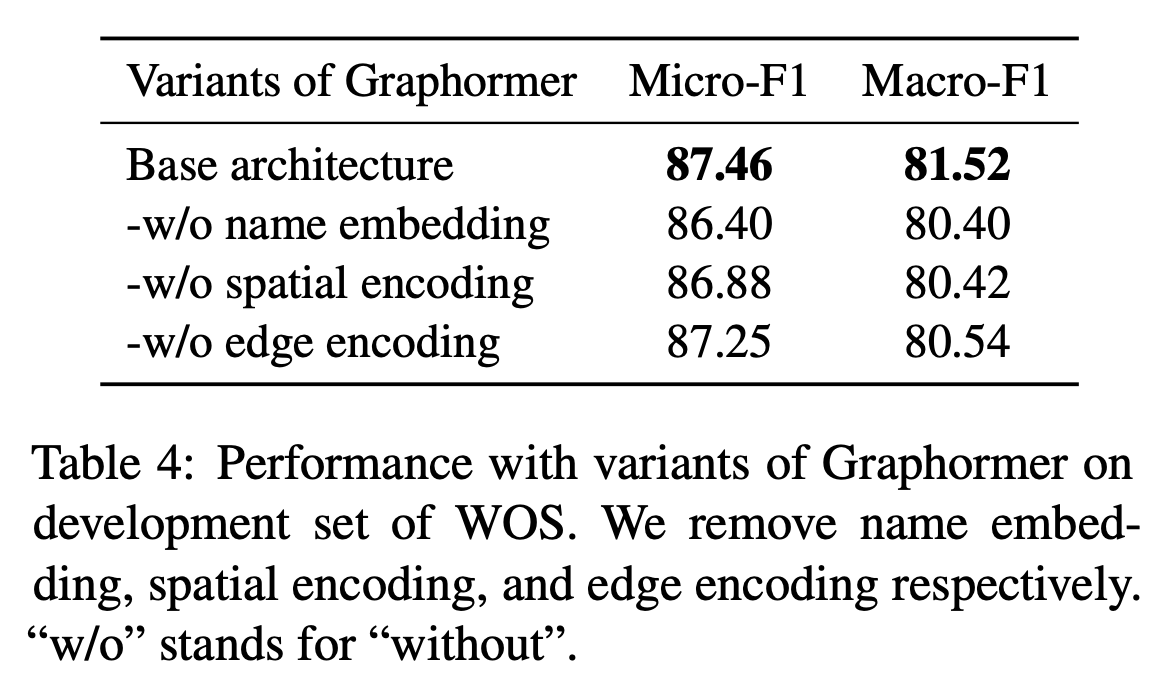
本文采用Graphormer建模标签的层次关系,在Transformer的基础上使用spatial encoding和edge encoding建模图结构。节点特征是标签嵌入和名称嵌入的和: \[ f_i = \mathrm{label\_emb}(y_i) + \mathrm{name\_emb}(y_i) \] 标签嵌入是可学习的,名称嵌入利用了标签的名称(其中可能蕴含了丰富信息),采用BERT编码得到,最终得到所有节点特征\(F\in\mathbb{R}^{k\times d_h}\)。
为了利用结构信息,采用Graphormer中魔改的self-attention \[ A_{ij}^{G} = \frac{(f_iW_Q^G)(f_jW_K^G)^T}{\sqrt{d_h}} + c_{ij} + b_{\phi(y_i, y_j)} \] 其中\(c_{ij} = \frac1D\sum_{n=1}^Dw_{e_n}\),\(D=\phi(y_i,y_j)\)。\(A_{ij}^G\)中的第一项是标准的点积注意力,\(c_{ij}\)表示edge encoding,\(\phi(y_i,y_j)\)表示两个节点间的距离。
因为在HTC问题中,图实际上是一个树,因此两个节点间只有一条路径\((e_1, e_2, \cdots, e_D)\),所以\(c_{ij}\)表示了两个节点间的边信息,\(w_{e_i}\in\mathbb{R}^1\)是可学习的权重。\(b_{\phi(y_i, y_j)}\)为spatial encoding,衡量了两个节点间的连通性。
和Transformer里一样,对注意力做softmax后LayerNorm即可。 \[ L = \mathrm{LayerNorm}(\mathrm{softmax}(A^G)V+F) \]
Positive Sample Generation
对于对比学习来说,最重要的就是构建正样本。这一步的目标是保留部分token,同时维持标签不变。对于BERT的token embedding来说: \[ \{e_1,e_2,\cdots,e_n\} = \mathrm{BERT\_emb}(x) \] 可以用cross attention衡量token与label之间的相关性 \[ q_i = e_iW_Q,k_j=l_jW_K,A_{ij}=\frac{q_ik_j^T}{\sqrt{d_h}} \] 其中\(W_Q, W_K\in\mathbb{R}^{d_h\times d_h}\)为权重矩阵。对注意力矩阵计算Softmax即可得到token \(x_i\)属于标签\(y_i\)的概率,给定\(y_j\)可以从分布中采样关键token,构建正样本\(\hat{x}\)。为了使得采样操作可微,采用Gumbel-Softmax代替Softmax。 \[ P_{ij} = \mathrm{gumbel\_softmax}(A_{i1},A_{i2},\cdots,A_{ik})_j \]
Gumbel-Softmax是一种重参数化(Reparameterization)的技巧,可以参考苏神的讲解。
将所有真实标签的概率相加,作为token \(x_i\)属于真实标签集合 \(y\)的概率 \[ P_i = \sum_{j\in y}P_{ij} \] 最终的正样本通过门限控制得到 \[ \hat{x} = \{x_i\ \text{if}\ P_i > \gamma\ \text{else}\ \mathbf{0}\} \] 其中\(\mathbf{0}\)表示全零向量,保持关键词的位置不变。因为选择操作也不可微,所以作者还给出了一种等价实现: \[ \hat{e_i} = e_i((P_i+Detach(1-P_i))\ \text{if}\ P_i > \gamma \ \text{else}\ 0) \] 其中\(\hat{e_i}\)要么为\(e_i\)要么为0,从而对应的梯度为 \[ \frac{\partial \hat{e}_i}{\partial P_i} = e_i\ \text{if}\ P_i > \gamma \ \text{else} \ 0 \] 将构建的正样本也送入BERT,得到表示 \[ \hat{H} = \mathrm{BERT}(\hat{x}) \]
Contrastive Learning Module
至此,已经有了文本序列和缩减字符的正样本,它们的句子表示应当相似。给定\(N\)个正样本对\((h_i,\hat{h_i})\),首先过一层全连接 \[ \begin{align} c_i &= W_2\mathrm{ReLU}(W_1h_i) \\ \hat{c_i} &= W_2\mathrm{ReLU}(W_1\hat{h_i}) \end{align} \] 其中\(W_1, W_2\in\mathbb{R}^{d_h\times d_h}\)。对于每个样本来说,同一个batch内的其他样本都是负例,所以共有\(2(N-1)\)个负样本对。之后和SimCSE一样,采用交叉熵计算 \[ \begin{equation} L_m^{con}=-\log\frac{\exp ({\rm sim}(z_m, \mu(z_m))/\tau)}{\sum^{2N}_{i=1,i\not= m}\exp ({\rm sim}(z_m, z_i)/\tau)} \end{equation} \] 其中\(\rm{sim}\)为cosine相似度,\({\rm sim}(u, v)=u\cdot v/ \|u\|\|v\|\),\(\mu\)为匹配函数: \[ \begin{equation} \mu(z_m)=\left\{ \begin{array}{ll} c_i, \text{ if } z_m=\hat{c_i}&\\ \hat{c_i}, \text{ if } z_m=c_i& \end{array} \right. \end{equation} \] 对比损失是所有样本的和 \[ \begin{equation} L^{con}=\frac{1}{2N}\sum_{m=1}^{2N}L_m^{con} \end{equation} \] 至于HTC任务,全连接+BCE即可。 \[ \begin{equation} L_{ij}^C=-y_{ij}\log(p_{ij})-(1-y_{ij})\log(1-p_{ij}) \end{equation} \]
\[ \begin{equation} L^C=\sum_{i=1}^N\sum_{j=1}^kL_{ij}^C \end{equation} \]
最终的损失函数是三者的加权和,在推理时模型退化为BERT+分类头。 \[ \begin{equation} L=L^C+\hat{L^C}+\lambda L^{con} \end{equation} \]
Experiment
选择了WOS、NYT和RCV1-V2数据集,使用bert-base-uncased作为基准模型。对于Graphormer,设置8个头,768的特征维度。batch size设置为12,学习率3e-5。
对于WOS,\(\gamma\)为0.02,对于NYT和RCV1-V2,\(\gamma\)为0.005。WOS和RCV1-V2的\(\lambda\)为0.1,NYT的\(\lambda\)为0.3。
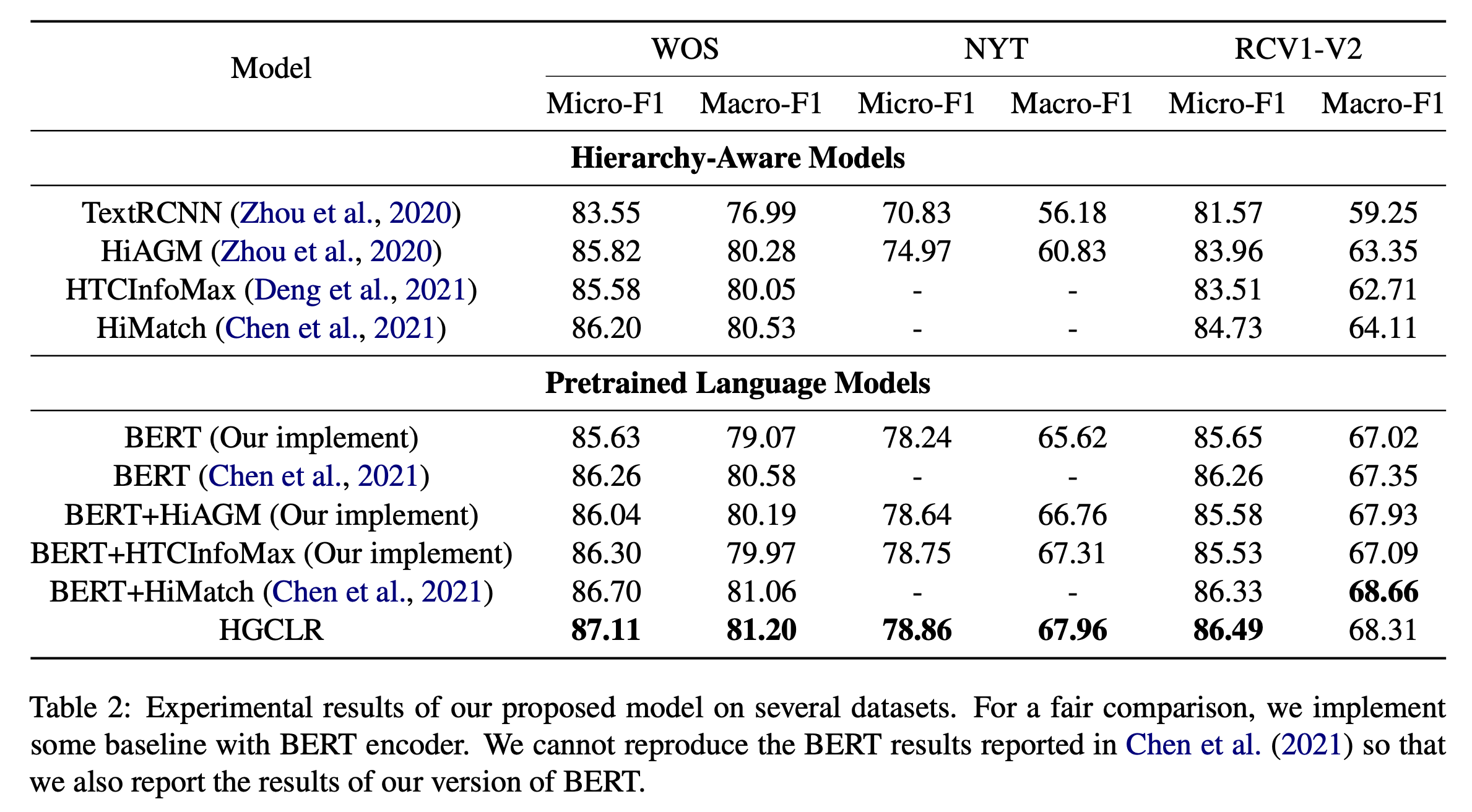
之前的部分模型采用TextRCNN作为文本编码器,作者也给出了BERT的结果。值得一提的是,作者没有复现出HiMatch的BERT结果,因此采用的是自己的结果。