Do Transformers Really Perform Bad for Graph Representation?
Graphormer:KDD Cup2021 OGB-LSC赛道的冠军方案
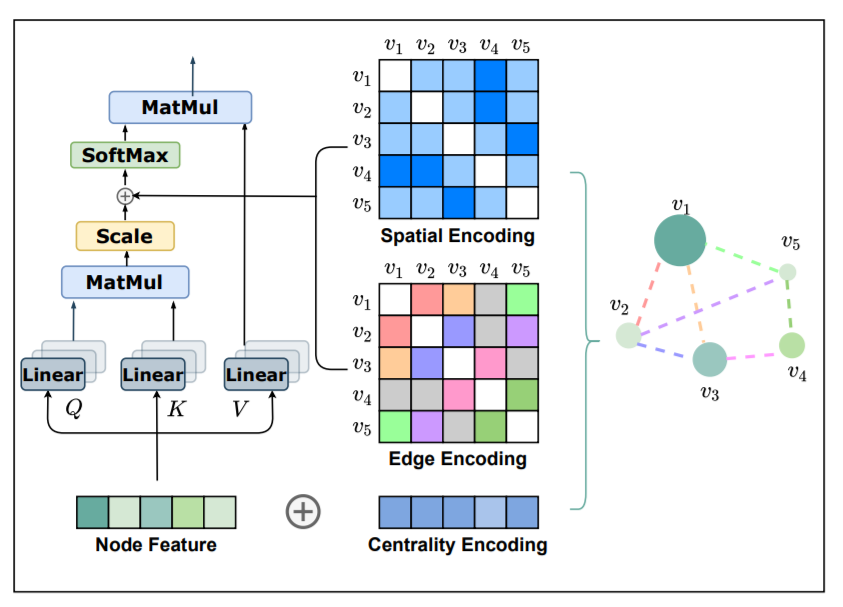
Overview
- KDD Cup2021: https://ogb.stanford.edu/kddcup2021
- Technical report: https://arxiv.org/pdf/2106.08279.pdf
- Arxiv: https://arxiv.org/pdf/2106.05234v3.pdf
- Code: https://github.com/microsoft/Graphormer/tree/ogb-lsc
来自大连理工和MSRA的一篇文章,值得一提的是Guolin Ke(https://github.com/guolinke)是TUPE的一作,也是尝试修改Transformer的工作。
Background
Transformer在NLP和CV都取得了成功,但在图表示学习任务上的表现还不尽如人意,不能匹敌GNN等图神经网络。本文提出了Graphormer,在原生Transformer的基础上改进,在许多图预测任务上取得了SOTA结果,包括OGB-LSC等。
原生Transformer适合序列建模,为了在图数据中发挥作用,需要在模型中融入图结构信息。本文的贡献如下:
- 提出了Centrality Encoding,以捕获图中节点的重要性。
- 提出了新颖的Spatial Encoding,捕获节点之间的结构关系。
- 在数学上证明了Graphormer有强大的表示能力,且GNN等变体可以看作Graphormer的特例。
Preliminary
GNN
对于图\(G=(V,E)\)来说,GNN旨在学习节点\(v_i\)的表示向量\(x_i\),采用聚合一阶或高阶邻居的表示迭代更新参数。
假设\(h_i^{(l)}\)为节点\(v_i\)在第\(l\)层的隐层表示,GNN的迭代过程主要有两步AGGREGATE和COMBINE: \[ \begin{align} a_i^{(l)} &= \mathrm{AGGREGATE}^{(l)}(\{h_j^{(l-1)}:j\in\cal{N}(v_i)\}) \\ h_i^{(l)} &= \mathrm{COMBINE}^{(l)}(\{h_j^{(l-1)}, a_i^{(l)}) \end{align} \] AGGREGATE聚合了邻居的信息,常用方法有MEAN、MAX、SUM等;COMBINE将聚合的信息融入节点表示。
此外,对于图表示任务,还需要设计READOUT函数,以用最后一层的节点特征\(h_i^{(L)}\)表示全图特征\(h_G\)。 \[ h_G = \mathrm{READOUT}(\{h_i^{(L)}|v_i\in G\}) \]
Transformer
老生常谈,主要分为前馈网络和自注意力两个部分,自注意力采用缩放点积和多头注意力。
Graphormer
Centrality Encoding
centrality意为中心地位,文章认为GNN中的聚合方式没有考虑节点在图中的重要性,比如名人在社交网络中具有更重要的影响因子。
在Graphormer中,根据入度和出度为每个节点赋予两个嵌入向量,在原来的节点特征上相加。 \[ h_i^{(0)} = x_i + z_{\mathrm{deg}^-}^- + z_{\mathrm{deg}^+}^+ \]
Spatial Encoding
Transformer可以捕获全局信息,但副作用是需要显示指定位置编码,比如序列数据中的绝对位置或相对位置编码。在图中,节点没有这种时序关系,为此设计了空间编码以捕获图结构信息。
具体来说,映射\(\phi(v_i,v_j):V\times V\rightarrow \mathbb{R}\)可以描述节点间的关系。如果节点相连,采用最短路径SPD,否则为给定值如-1。本文采用可学习的标量,并作为自注意力模块中的偏置项。 \[ A_{ij} = \frac{(h_iW_Q)(h_jW_K)^T}{\sqrt{d}}+b_{\phi(v_i,v_j)} \] 其中,\(A_{ij}\)为注意力的权重矩阵。
Edge Encoding in the Attention
除此之外,本文还考虑了边的结构信息。一种方式是直接将边特征与节点特征相加,另一种方式则是在聚合的时候考虑边的特征。但这些方法只向相关节点传播信息,不能有效利用全局信息。
对于有序节点对\((v_i, v_j)\),寻找最短路径\(SP_{ij}=(e_1,e_2,\dots,e_N)\),对于均值计算点积作为编码: \[ c_{ij} = \frac1N\sum_{n=1}^{N}x_{e_n}(w_n^E)^T \] 将编码结合在自注意力中 \[ A_{ij} = \frac{(h_iW_Q)(h_jW_K)^T}{\sqrt{d}}+b_{\phi(v_i,v_j)} + c_{ij} \]
Implementation
Special Node
BERT中设计了[CLS]用于代表序列的全局信息,本文也设计了类似的节点[VNode],将最后一层的节点特征作为全局表示\(h_G\)。不同于[CLS]放在句首,[VNode]与所有节点相连,但要区分空间编码\(b_{\phi([VNode],v_i)}\)和\(b_{\phi(v_i, [VNode])}\)。
Experiment
首先在OGB-LSC上,进行了实验结果的比较,数据集为量子化学回归PCQM4M-LSC,总共包含3.8M的图。
参数方面,提供了两个版本,分别采用12层768维和6层512维。
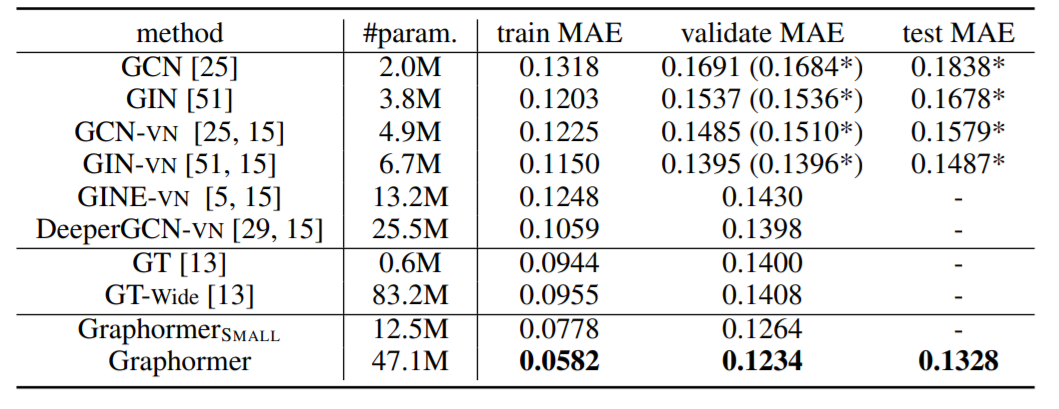
本文还在MoIPCBA、MoIHIV和ZINC上做了实验,都取得了较好的结果,数据集详情如下。

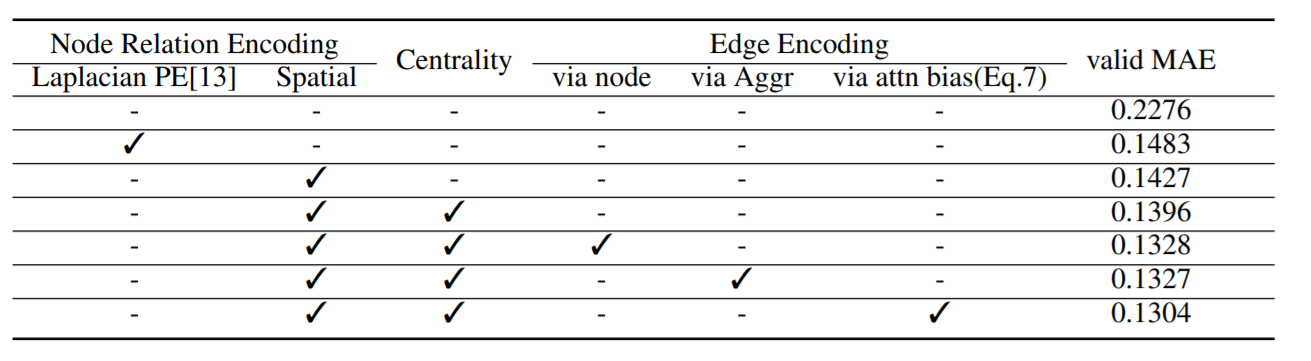
本文也做了消融实验,验证各个模块的有效性。