Combining Label Propagation and Simple Models Out-performs Graph Neural Networks
ICLR 2021,采用后处理的方法而非GNN在OGB上取得SOTA。
Overview

- paper: https://arxiv.org/pdf/2010.13993.pdf
- code: https://github.com/CUAI/CorrectAndSmooth
Background
随着图神经网络变得越来越复杂, 理解模型的性能为什么提升越来越困难,将其应用在大规模数据集上也很困难。
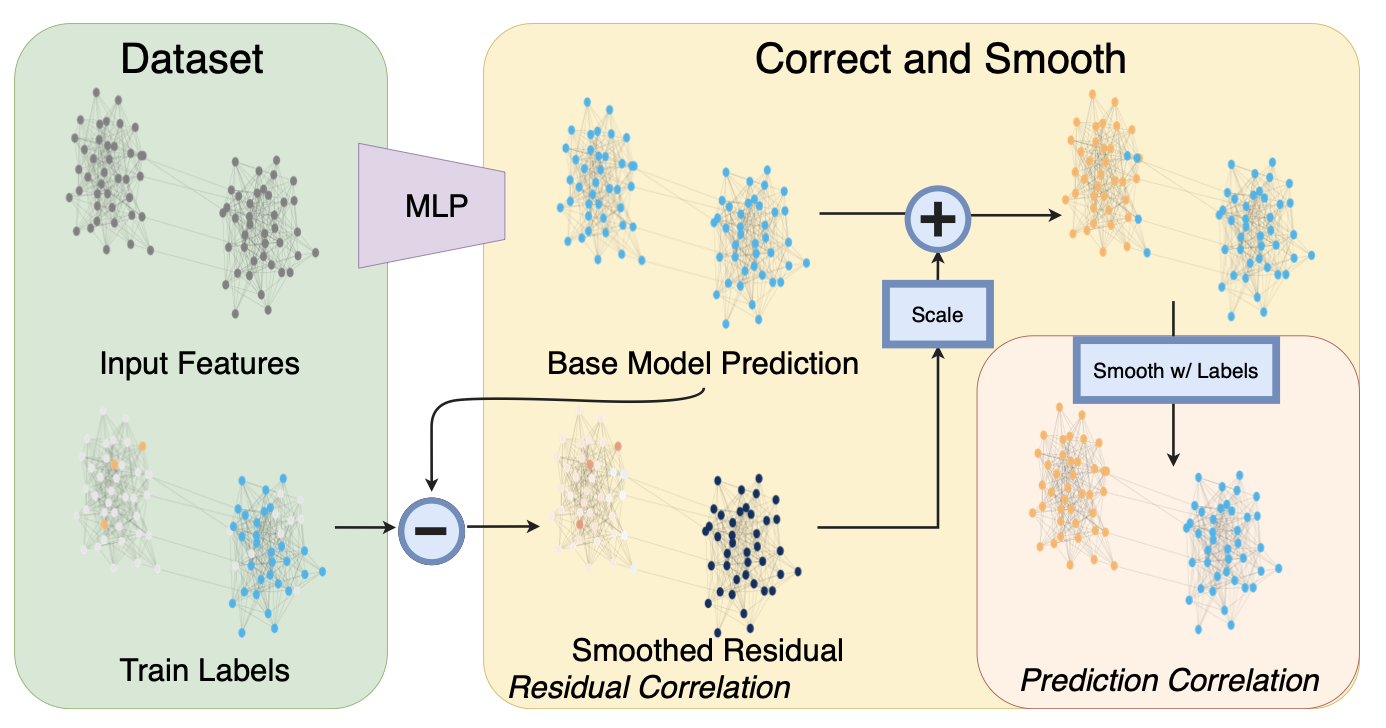
本文提出了一个简单的pipeline,包括三个部分
- 忽略图结构,用节点特征进行基本预测。
- 纠正步骤,将训练数据的不确定性传播到整个图中,以纠正基本预测。
- 对预测结果进行平滑处理。
步骤2和3仅仅采用了经典方法做后处理。
Method
图\(G=(V,E)\)有\(n=|V|\)个节点,节点特征\(X\in\mathbb{R}^{n\times p}\)。\(A\)为邻接矩阵,\(D\)为对角度矩阵,\(S=D^{-1/2}AD^{-1/2}\)。对于预测问题,节点集合分为有标注的\(L\)和无标注的\(U\),标签\(Y\in\mathbb{R}^{n\times c}\),需要给未标注的节点\(j\in U\)打标签。
首先直接用MLP对节点特征预测,不依赖任何的图结构,得到基本预测\(Z\)。
然后考虑融入标签特征纠正错误,提升预测的准确率。首先定义错误矩阵\(E\in\mathbb{R}^{n\times c}\),在验证集和测试集上均为0。 \[ E_{L_t} = Z_{L_t} - Y_{L_t},\quad E_{L_v}=0,\quad E_{U}=0. \] 采用标签传播(label spreading)技巧对错误进行平滑,优化目标为 \[ \hat{E} = \arg \min_{W\in\mathbb{R}^{n\times c}} \trace(W^T(I-S)W)+\mu\lVert W-E\rVert^2_F \] 第一项平滑了错误,第二项保障了所求的解接近初始错误。可以通过迭代求解\(E^{(t+1)} = (1-\alpha)E+\alpha SE^{(t)}\),其中\(\alpha=1/(1+\mu)\),\(E^{(0)} = E\)。从而平滑后的错误为 \[ Z^{(r)} = Z + \hat{E} \] 这种传播在回归问题的高斯假设下被证明正确,但对于分类问题而言,平滑后的错误可能尺度\(\hat{E}\)不对。可以推出 \[ \lVert E^{(t+1)}\rVert \le (1-\alpha)\lVert E\rVert + \alpha\lVert S\rVert_2\lVert E^{(t)}\rVert_2 = (1-\alpha)\lVert E\rVert_2 + \alpha\lVert E^{(t)}\rVert_2 \] 当\(E^{(0)} = E\),从而\(\lVert E^{(t)}\rVert_2\le\lVert E\rVert_2\)。因此传播不能完全纠正图中节点的错误,本文提出了两种缩放机制Autoscale和Scaled Fixed Diffusion来处理这个问题。
在得到得分向量\(Z^{(r)}\)后,进一步对预测结果进行平滑。这是因为邻接的节点容易有相同的标签,所以采用标签传播再一次平滑处理。 \[ G_{L_t} = Y_{L_t},\quad G_{L_v,U} = Z_{L_v, U}^{(r)} \] 将训练节点设置为真实标签,验证与无标注节点采用纠正预测(验证集也可以用真实标签)。采用\(G^{(t+1)} = (1-\alpha)G+\alpha SG^{(t)}\)迭代,给出最终的预测结果\(\hat{Y}\)。
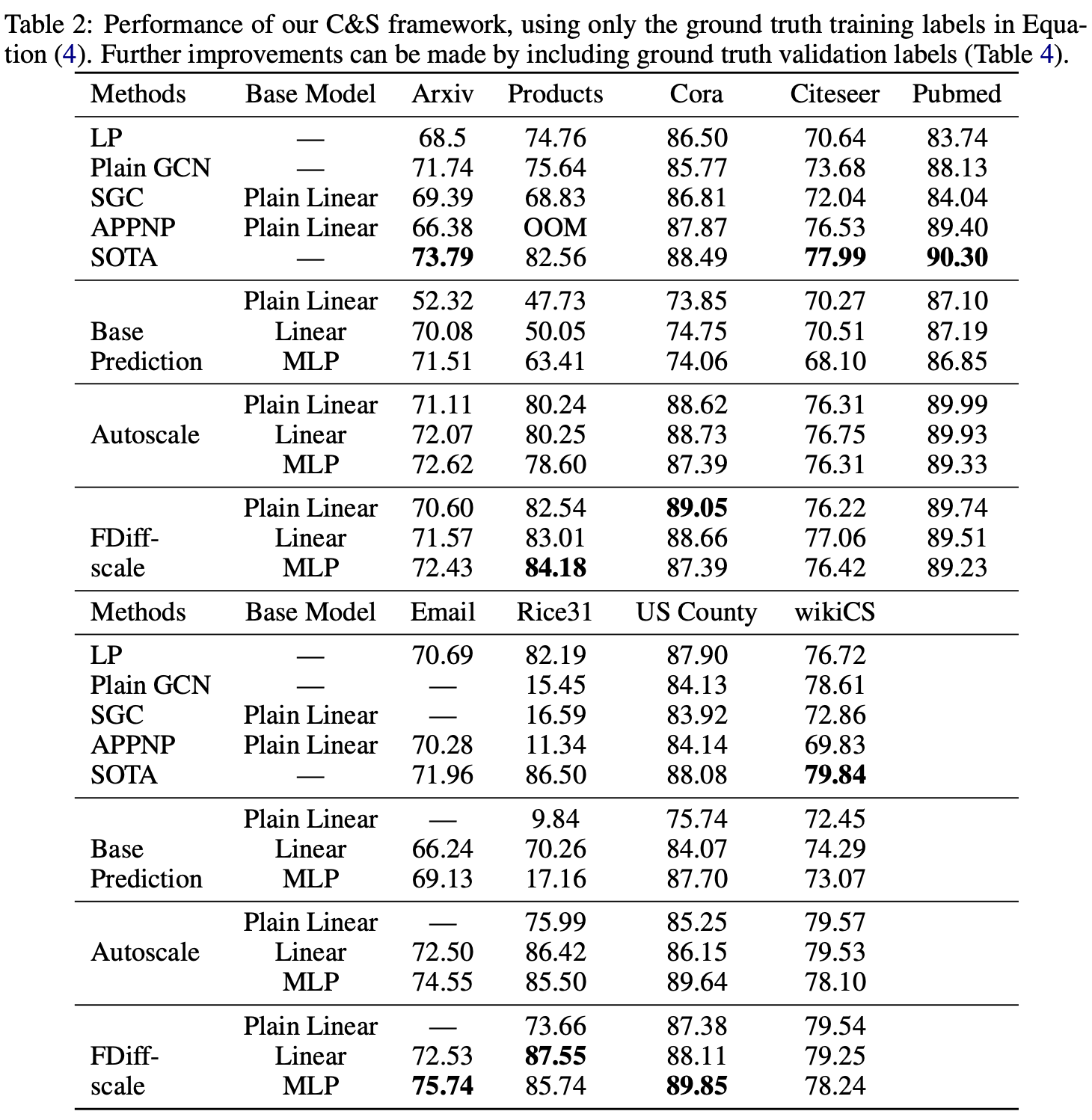
Experiment