Laplace Redux -- Effortless Bayesian Deep Learning

发表于 更新于 分类于 阅读次数：
本文字数： 3.6k

NIPS 2021，拉普拉斯近似（Laplacian Approximation）。

Overview

image-20220221150455582

Background

现代神经网络有几个缺点

  • 校准能力差，过度自信（overconfidence）。
  • 持续训练时对先前任务的灾难性遗忘（catastrophic forgetting）。
  • 选择合适的网络架构和超参数很困难。

贝叶斯模型为解决这些问题，采取了如下措施：

  • 给模型配备鲁棒的不确定估计。
  • 捕获过去的信息，使得模型能够持续学习。
  • 通过在数据拟合和模型复杂度间寻找最优的trade-off，实现自动的模型选择。

贝叶斯神经网络介绍：https://zhuanlan.zhihu.com/p/81170602

但是贝叶斯神经网络并没有投入实施，主要是因为其难以实现和调参，训练代价大，很难scale到现代的模型和数据集。

本文认为，拉普拉斯近似（Laplace Approximation，LA）是贝叶斯深度学习中一种简单高效，同时有竞争力的近似方法。

  • 本文率先调研了深度学习中LA的发展，并展现了可扩展且实用的LA的关键要素。
  • 提供了基于Pytorch的LA库laplace，实现了大量LA变种。
  • 使用laplace库进行了大量实验，展现了LA的竞争力。

Method

Laplace Approximation in Deep Learning

深度学习中，LA有两种方式使用：

  1. 采用LA近似模型的后验分布，使得模型能够概率预测。
  2. 使用LA近似model evidence，从而可以模型选择（调超参数）。

给定数据集\(\mathcal{D} := \{ (x_n \in \mathbb{R}^M, y_n \in \mathbb{R}^C)\}\)，参数为\(\theta\in\mathbb{R}^D\)，\(L\)层的神经网络\(f_\theta:\mathbb{R}^M\rightarrow \mathbb{R}^C\)旨在最小化经验风险，通常可以分解为经验损失项\(\ell(x_n,y_n;\theta)\)和正则项\(r(\theta)\)的和。 \[ \theta_{MAP} = \arg\min_{\theta\in\mathbb{R}^D}\mathcal{L}(D;\theta) = \arg\min_{\theta\in\mathbb{R}^D}\left(r(\theta) + \sum_{n=1}^N\ell(x_n,y_n;\theta)\right) \] 从贝叶斯的角度来看，这些项可以看作独立同分布的对数似然（log-likelihood）和对数先验（log-prior），此时\(\theta_{MAP}\)事实上就是最大后验估计（Maximum A Posteriori, MAP）。 \[ \ell(x_n,y_n;\theta) = -\log p(y_n|f_\theta(x_n))\qquad \text{and} \qquad r(\theta) = -\log p(\theta) \] 广泛使用的正则方法\(r(\theta)= \frac{1}{2} \gamma^{-2}\|\theta\|^2\)（也被称为权重衰减），对应一个中心的高斯先验\(p(\theta)=\mathcal{N}(\theta;0,\gamma^2 I)\)。训练损失取负后的指数\(\exp(-\mathcal{L}(\mathcal{D};\theta))\)就相当于未归一化的后验，归一化后可得 \[ \begin{equation} p(\theta \mid \mathcal{D}) = \tfrac{1}{Z} \,p(\mathcal{D} \mid \theta) \, p(\theta) = \tfrac{1}{Z}\exp(-\mathcal{L}(\mathcal{D};\theta)), \qquad Z:= \textstyle\int p(\mathcal{D} \mid \theta) \, p(\theta) \,d\theta \end{equation} \] 拉普拉斯近似用一个\(\mathcal{L}\)的二阶展开去构造对\(p(\theta|\mathcal{D})\)的高斯近似，因此考虑 \[ \begin{equation} \mathcal{L}(\mathcal{D}; \theta) \approx \mathcal{L}(\mathcal{D}; \theta_\text{MAP}) + \tfrac{1}{2} (\theta - \theta_\text{MAP})^\intercal \left( \nabla^2 _\theta \mathcal{L}(\mathcal{D}; \theta) \vert_{\theta_\text{MAP}} \right)(\theta - \theta_\text{MAP}) , \end{equation} \] 其中一阶项在\(\theta_{\text{MAP}}\)处消失，从而可以将其看作高斯分布，即拉普拉斯后验近似： \[ \begin{equation} p(\theta \mid \mathcal{D}) \approx \mathcal{N}(\theta; \theta_\text{MAP}, \varSigma) \qquad\text{with}\qquad \varSigma := -\left( \nabla^2_\theta \mathcal{L}(\mathcal{D};\theta) \vert_{\theta_\text{MAP}} \right)^{-1}. \end{equation} \] 归一化常数\(Z\)（通常被称为marginal likelihood或evidence）可用于模型选择，可以通过下式近似： \[ Z \approx \exp(-\mathcal{L}(\mathcal{D};\theta_\text{MAP})) \, (2\pi)^{D/2} \, (\det \varSigma)^{1/2} \] \(\theta_{\text{MAP}}\)可以通过标准的深度学习得到，唯一的额外步骤就是计算Hessian矩阵在\(\theta_{\text{MAP}}\)处的逆。因此在得到预训练模型后，可以离线计算LA。

一般来说，具有两次微分后对数密度的先验都可以使用。由于权重衰减的广泛使用，本文假设先验是零均值的高斯分布\(p(\theta)=\mathcal{N}(\theta;0,\gamma^2 I)\)。从而Hessian矩阵取决于对数先验的正则器，以及复杂的对数似然。 \[ \begin{equation} \nabla^2_\theta \mathcal{L}(\mathcal{D};\theta) \vert_{\theta_\text{MAP}} = -\gamma^{-2} I - \textstyle\sum_{n=1}^N \nabla^2_\theta \log p(y_n \mid f_\theta(x_n)) \vert_{\theta_\text{MAP}}. \end{equation} \] Hessian矩阵之所以没有简单实现，就是因为式中第二项随着网络参数的规模平方增长。

Four Components of Scalable Laplace Approximation

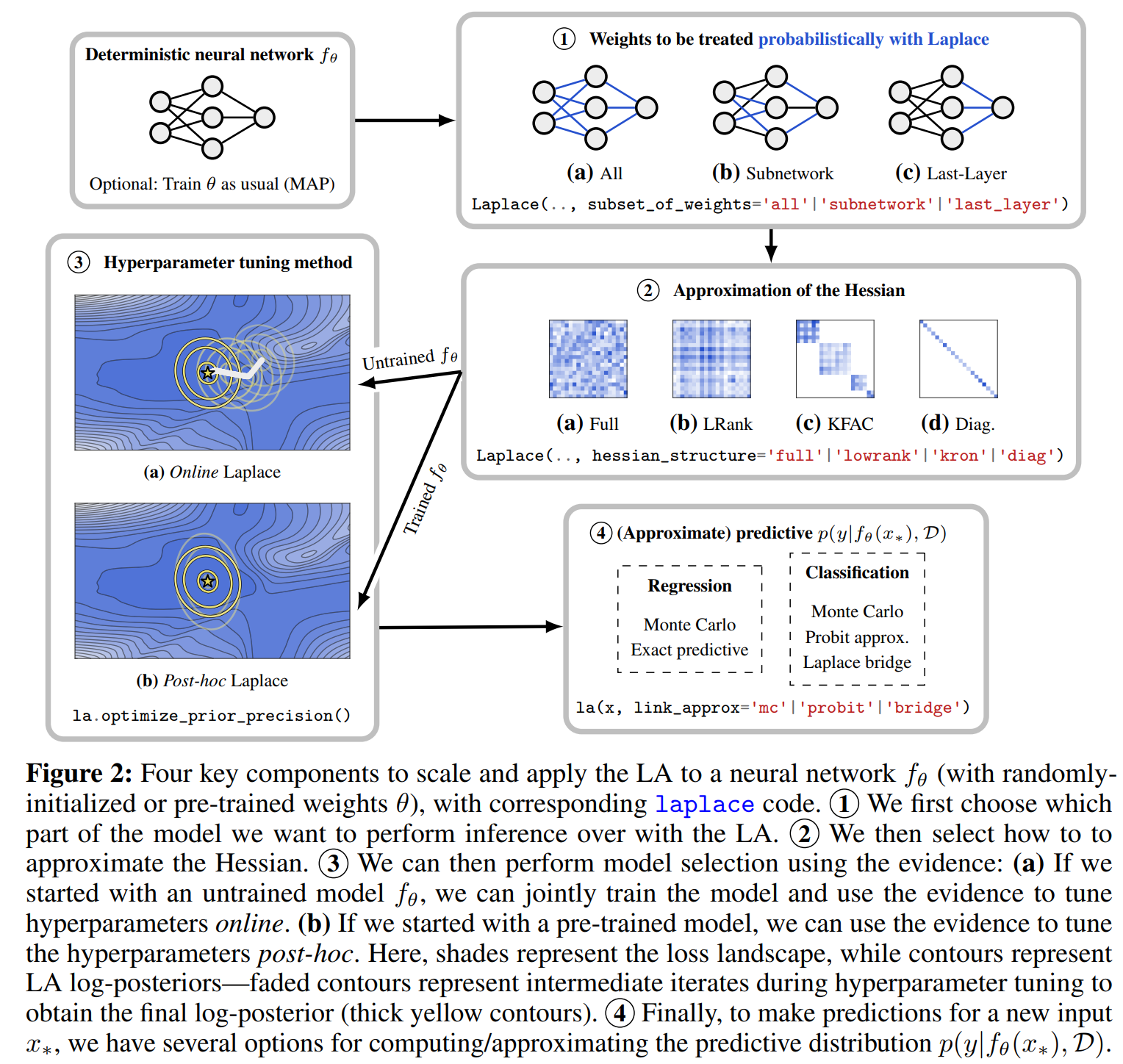
image-20220222101329285

laplace: A Toolkit for Deep Laplace Approximation

image-20220222101713332

Experiments

本文的实验分为四个部分

  1. 寻找LA的最佳设计选择。
  2. 在in-distribution、dataset-shift和out-of-distribution三种设置下，验证LA相比于贝叶斯baseline的竞争力。
  3. 展现LA适用于各种数据模态和网络架构（包括transformer），这种情况下贝叶斯方法难以使用。
  4. 展示LA可以作为持续学习的一个易用baseline。

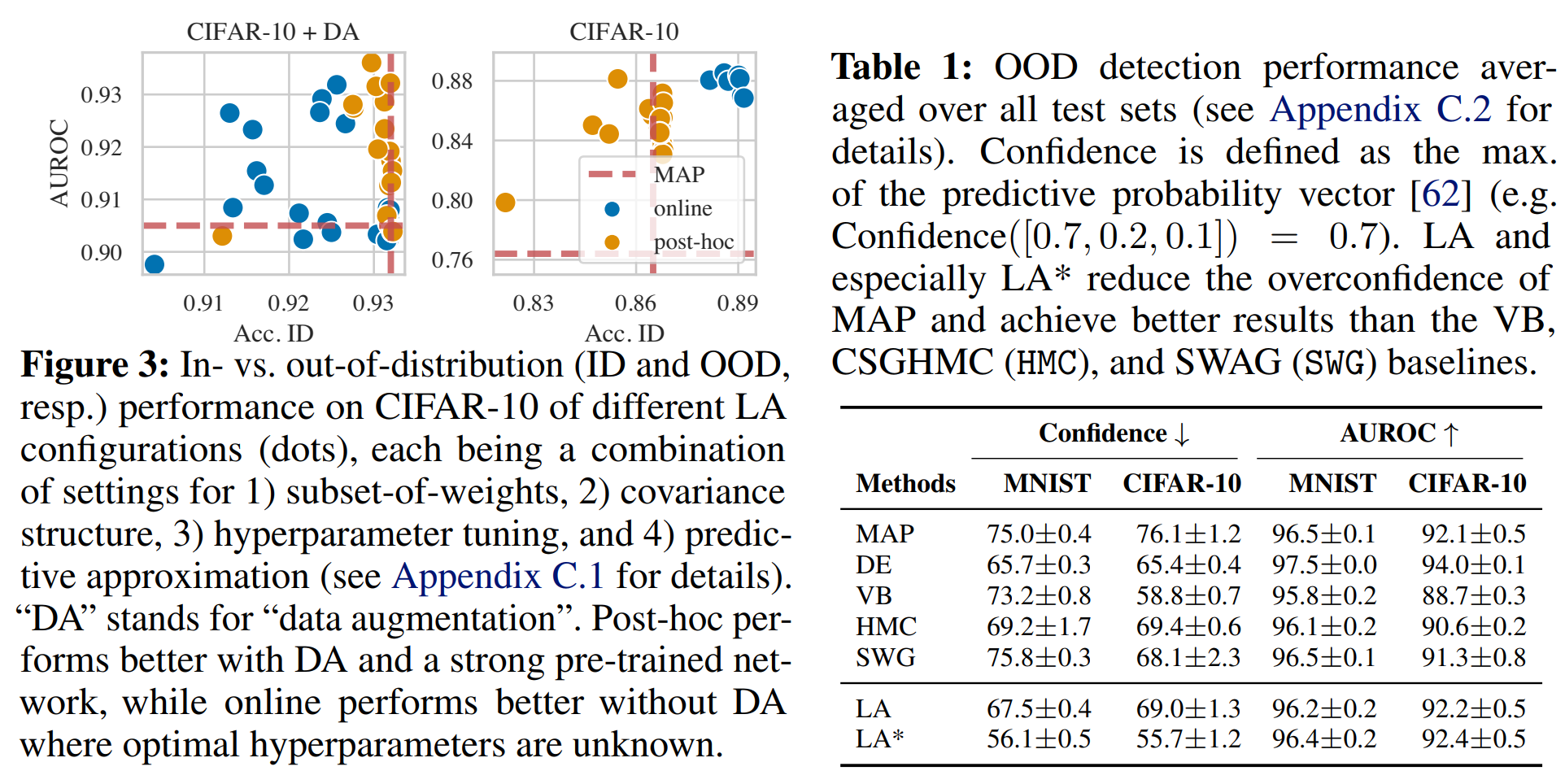
image-20220222103811412

实验结果表明，在CIFAR-10有数据增强的情况下，后处理的LA表现更好。

laplace中默认设置是一个后处理KFAC最后一层的LA，采用GGN近似Hessian矩阵。这适用于所有最后一层为全连接层的网络架构，因此适用于预训练网络。对于需要自己训练的模型，采用GGN或经验Fisher的在线KFAC LA是一个不错的baseline。