Multi-label Classification with Partial Annotations using Class-aware Selective Loss
分析了多标签分类中的部分标注问题,设计了Loss函数处理这个问题。
Overview

- paper: https://arxiv.org/pdf/2110.10955v1.pdf
- code: https://github.com/alibaba-miil/partiallabelingcsl
- dataset: OpenImages LVIS MS-COCO
Background
近年来,对每张图像进行完整标注变得越来越困难。例如OpenImages的训练集有900万张图像,包含9600个类别。在现实的大规模多标签分类任务中,部分标注的数据是不可避免的,如何处理那些未标注的标签是一个问题。
最简单的方法就是直接忽略未标注的标签,但这样只利用了数据的一部分。将其直接当作负标签也是一种方法,但会引入噪声,并加剧正负样本的不平衡。这两种方法分别对应于下图的b和c。
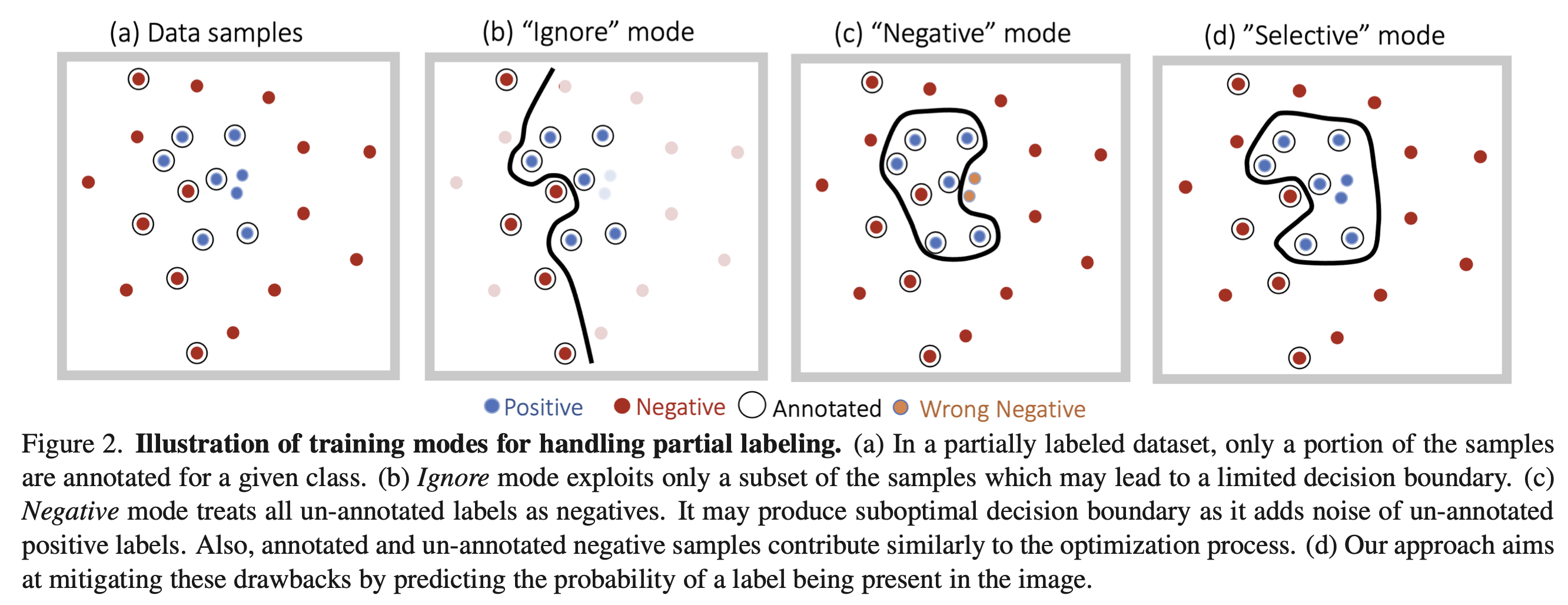
OpenImages中“黑色”标签只标注了1688个样本,占全体样本的0.02%,然而这是很可能频繁出现的标签。因此统计数据集中类别的频数往往不能反映真实的标签比例,需要从数据中估计类别的分布。
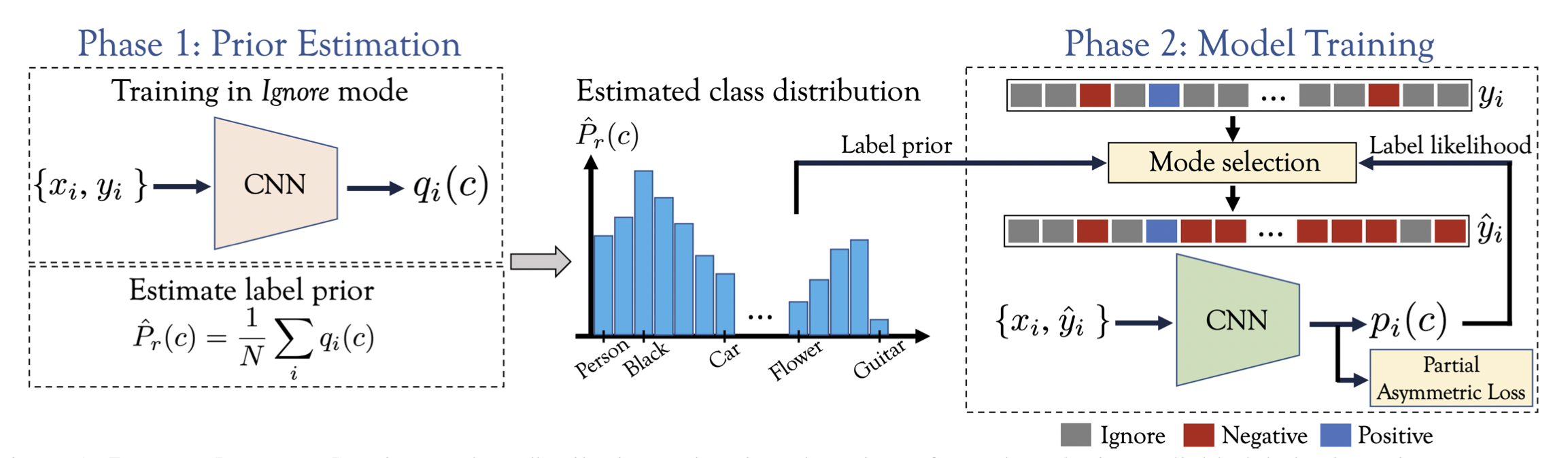
本文提出了选择性(Selective)的方法,利用标签概率(Label likelihood)和标签先验(Label prior)两项判断每个标签的模式(Ignore还是Negative)。为了获得一个可靠的标签先验,还提出了一种估计类别分布的方法。
Method
给定部分标注的多标签数据集,类别标签\(y_c\in\{-1,0,1\}\),其中0表示缺失。用\(\mathcal{P}_{\mathbf{x}}=\{c|y_c=1\}\)和\(\mathcal{N}_{\mathbf{x}}=\{c|y_c=-1\}\)分别表示正负标签,用\(\mathcal{U}_{\mathbf{x}}=\{c|y_c=1\}\)表示未标注的类别,通常有\(|\mathcal{P}_{\mathbf{x}}\cup \mathcal{P}_{\mathbf{x}}|\ll|\mathcal{U}_{\mathbf{x}}|\)。损失函数的通用形式可以定义如下: \[ \mathcal{L}(x) = \sum_{c\in\mathcal{P}_{\mathbf{x}}}\mathcal{L}^+(\mathbf{x}) + \sum_{c\in\mathcal{N}_{\mathbf{x}}}\mathcal{L}^-(\mathbf{x}) + \sum_{c\in\mathcal{U}_{\mathbf{x}}}\mathcal{L}^u(\mathbf{x}) \] 对于常见的BCE,只考虑标注数据则有\(\mathcal{L}^+(\mathbf{x})=\log(p_c)\),\(\mathcal{L}^-(\mathbf{x})=\log(1-p_c)\),\(\mathcal{L}^u(\mathbf{x})=0\)。
对于Ignore模式,即有\(\mathcal{L}^u(\mathbf{x})=0\);对于Negtive模式,即有\(\mathcal{L}^u(\mathbf{x})=\mathcal{L}^-(\mathbf{x})\)。
本文采用非对称损失ASL(Asymmetric Loss)作为基准,其能够动态关注困难样本同时控制正负样本传播的比例。对于基本的Focal Loss,有 \[ \mathcal{L}_F(p_c,\gamma) = (1-p_c)^\gamma\log p_c \] 部分非对称损失P-ASL定义为 \[ \begin{align} \mathcal{L}(x) = &\sum_{c\in\mathcal{P}_{\mathbf{x}}}\mathcal{L}_F(p_c, \gamma^+)\\ +&\sum_{c\in\mathcal{N}_{\mathbf{x}}}\mathcal{L}_F(1-p_c,\gamma^-) +\sum_{c\in\mathcal{U}_{\mathbf{x}}}\omega_c\mathcal{L}_F(1-p_c, \gamma^u) \end{align} \] 通常设置\(\gamma^+<\gamma^-\),因为正样本更少见。同时有\(\gamma^-<\gamma^u\),因为有标注的负样本更值得信赖。
Class-aware Selective Loss
标签概率表示未标注标签\(c\)的概率 \[
P(y_c=1|\mathbf{x};\mathbf{\theta});\quad\forall c\in\mathcal{U}_{\mathbf{x}}
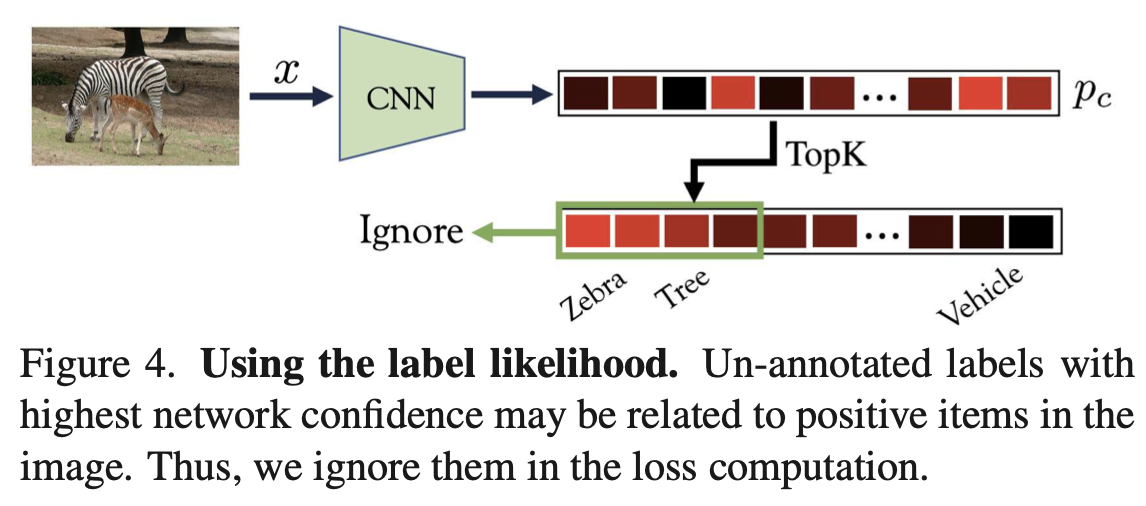
\] 高置信度的标签可能出现在图像中,不能将其当作负样本,应该忽略。为此作者选了\(K\)个最高概率的标签: \[
\Omega_L = \{c\in\mathcal{U}_{\mathbf{x}}|c\in\text{TopK}(\{p_c\})\}
\] 
标签先验可以看作数据中标签的出现频率 \[ P(y_c=1);\quad\forall c\in\mathcal{U}_{\mathbf{x}} \] 用\(\hat{P}_r(c)\)表示先验估计器,我们对于高先验值的标签感兴趣。 \[ \Omega_P = \{c\in\mathcal{U}_{\mathbf{x}}|\hat{P}_r(c)>\eta\} \] 其中\(\eta\in[0,1]\)表示是否忽略的阈值。 \[ O_{\text{Ignore}} = \Omega_{L}\cup\Omega_P \] 相应地,对应的权重定义为 \[ \omega_c = \begin{cases} 0 & c\in\Omega_{\textrm{Ignore}} \\ 1 & c\notin\Omega_{\textrm{Ignore}} \end{cases} \]
Estimating the Class Distribution
在MS-COCO中,89%的类别出现在少于5%的样本中。标签先验可以通过下式估计 \[ P(y_c=1;\theta) = \frac{1}{|\mathcal{X}|}\sum_{\mathbf{x}\in\mathcal{X}}P(y_c=1|\mathbf{x};\mathbf{\theta}) \] 在Ignore模式下训练模型,此时则有\(\hat{P}_r(c) = P(y_c=1;\mathbf{\theta}_{\text{Ignore}})\)。
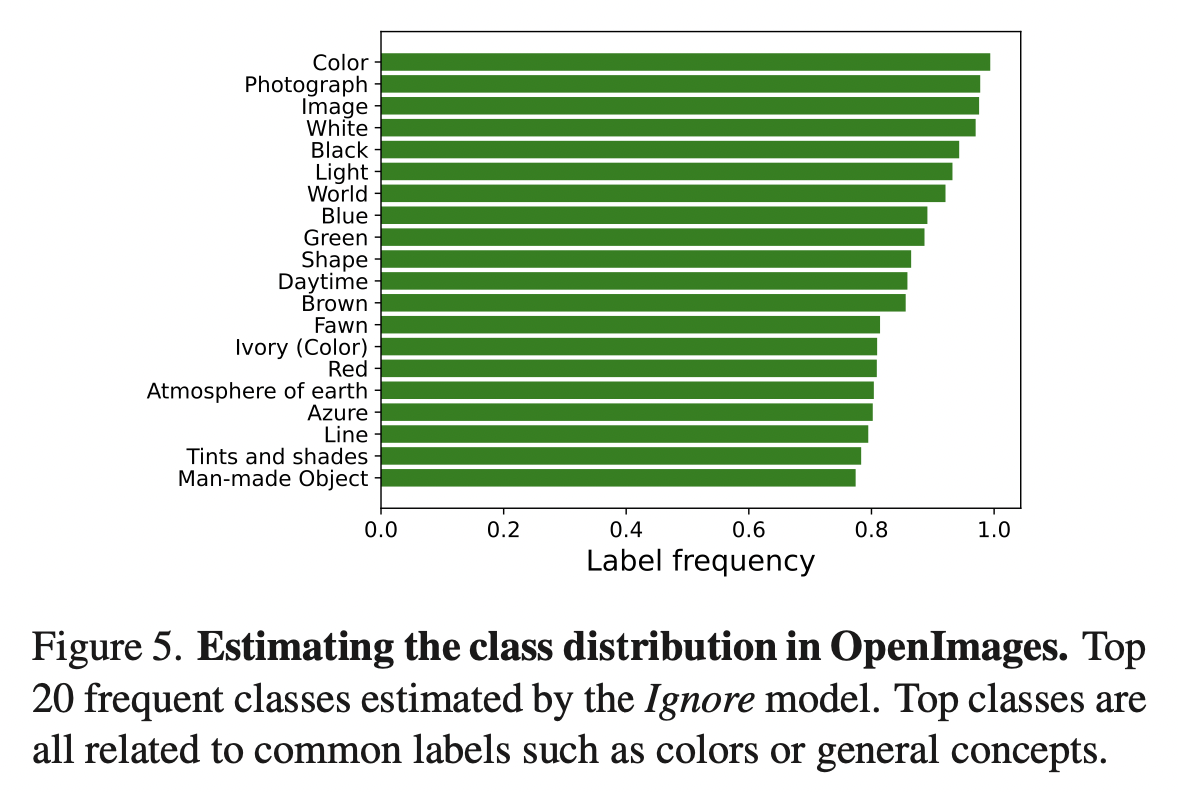
Experiment
采用完整标注的MS-COCO数据集,模拟部分标注进行实验。部分标注的模式有两种:
- Fixed per class (FPC) 对于每个类别随机采样固定数目\(N_s\)的正负标注,丢弃其余标注。
- Random per annotation (RPA) 按概率\(p\)删除每个标注。
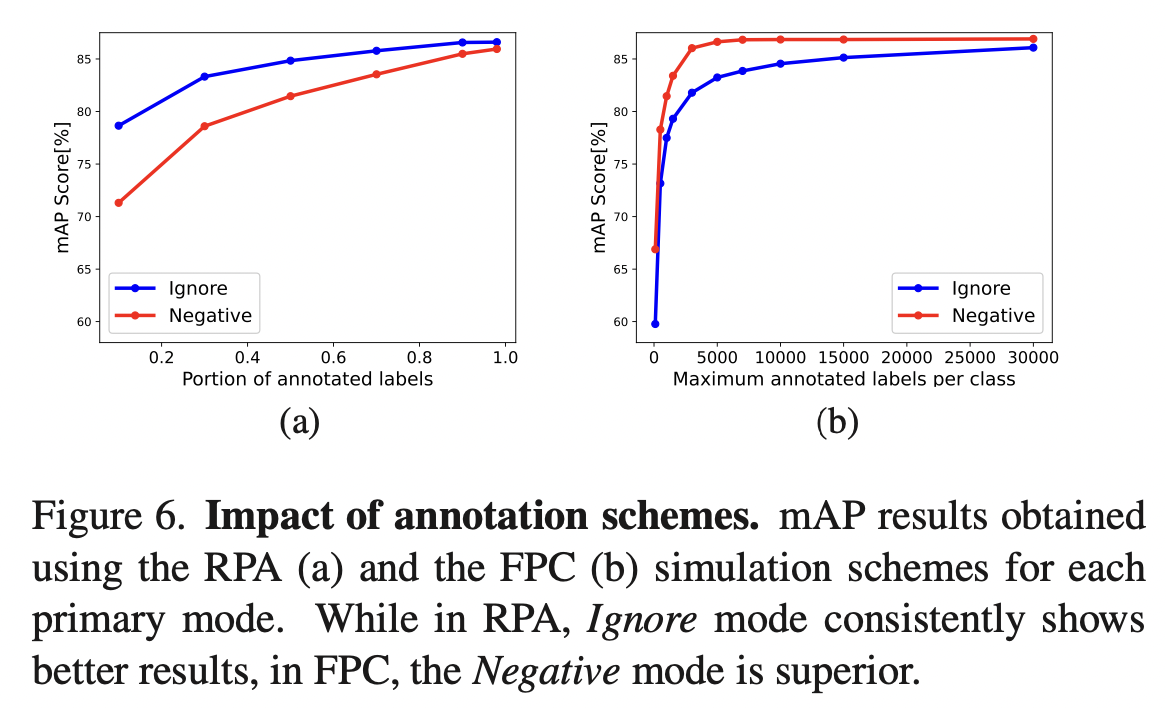
作者比较了估计的标签分布与实际分布的相似度,可以看出Ignore模式更适合。
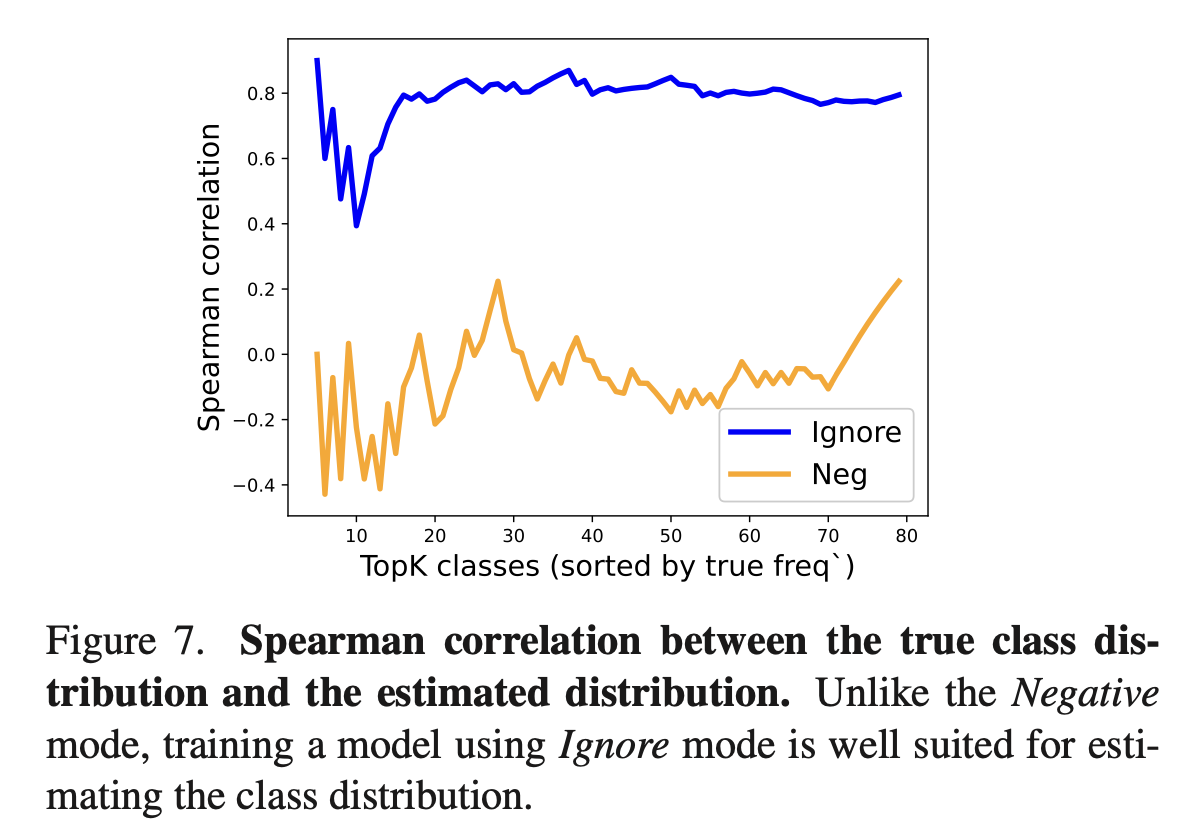
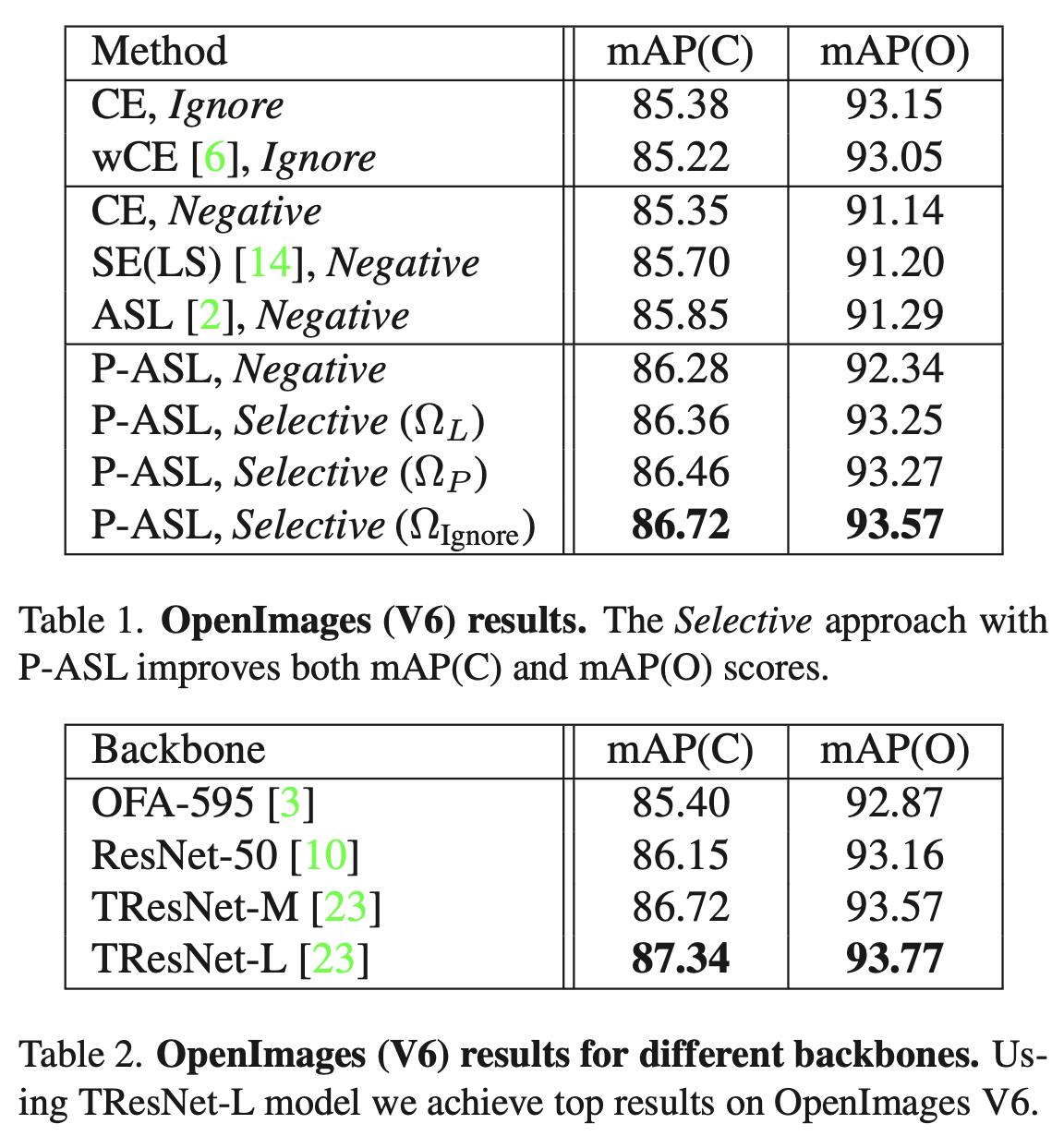
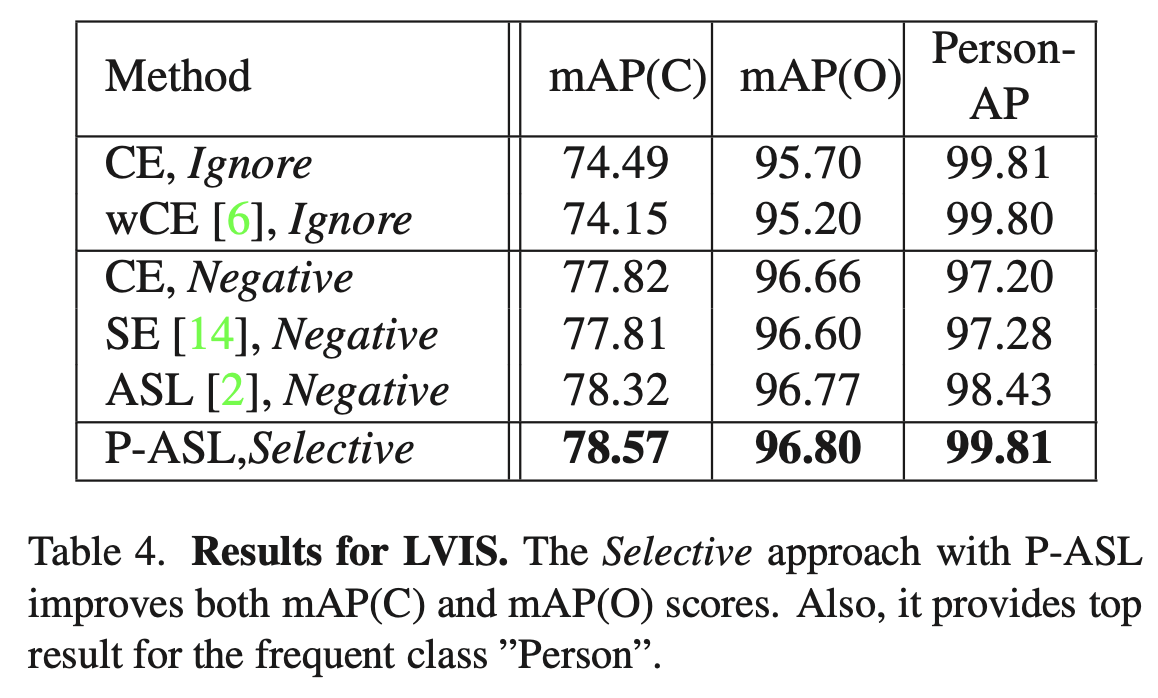
公开benchmark选择了OpenImages和LVIS,取得了SOTA结果。