HCL-MTC: Hierarchical Contrastive Learning for Multi-label Text Classification
ACL ARR 2022,提出层次对比学习,学习标签间的区别信息。
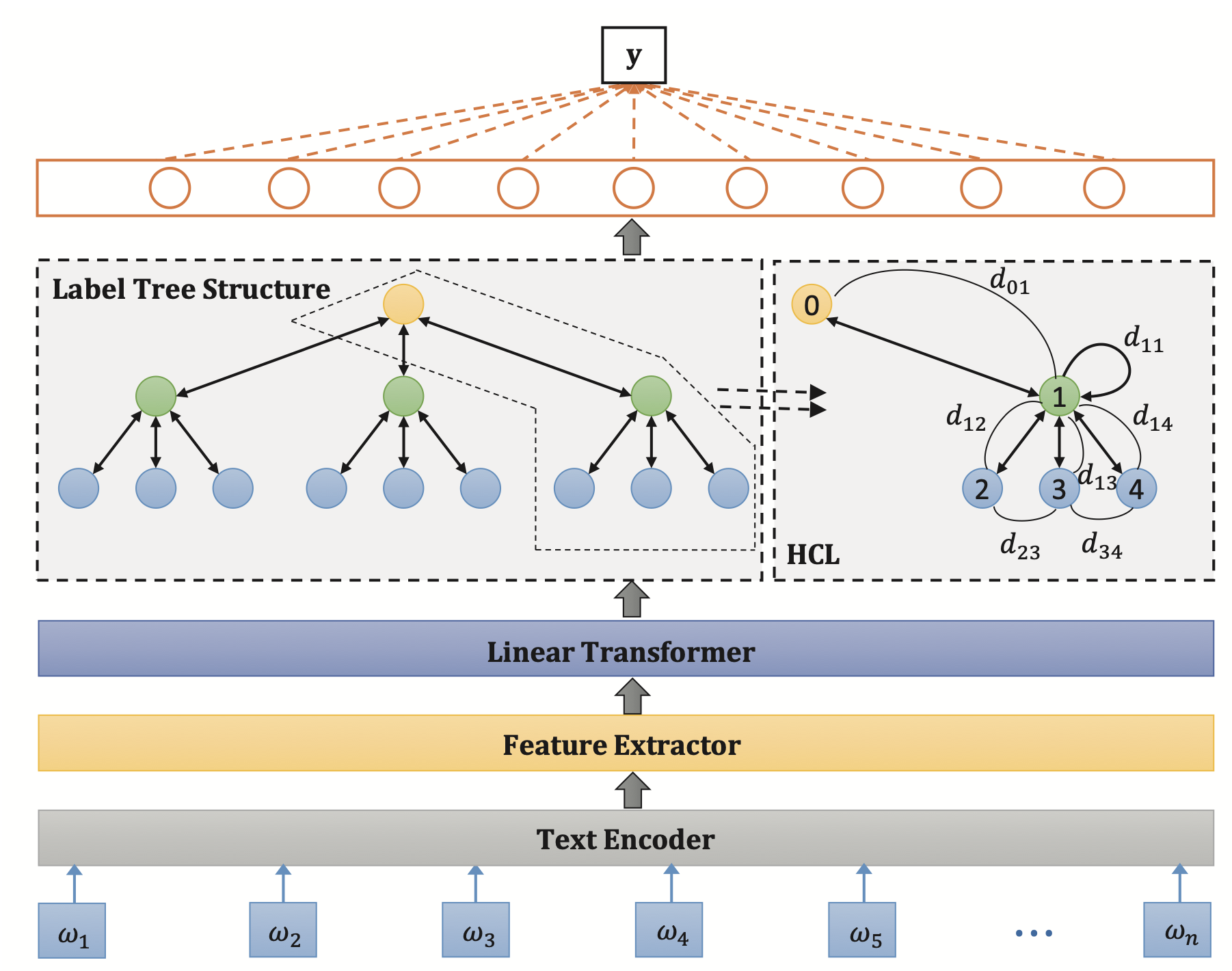
Overview
- paper: https://openreview.net/pdf?id=R1BifFIieBP
- code:
- dataset: RCV1-V2 Wos
Background
MLTC任务可以分为两种方法:直接从文本信息预测以及从文本标签的混合信息中预测。前者忽略了标签间的信息,后者可以学习标签的层次信息。
作者认为现有方法没有充分利用标签信息,只考虑了相关信息(correlative information),忽略标签的区别信息(distinctive information)。
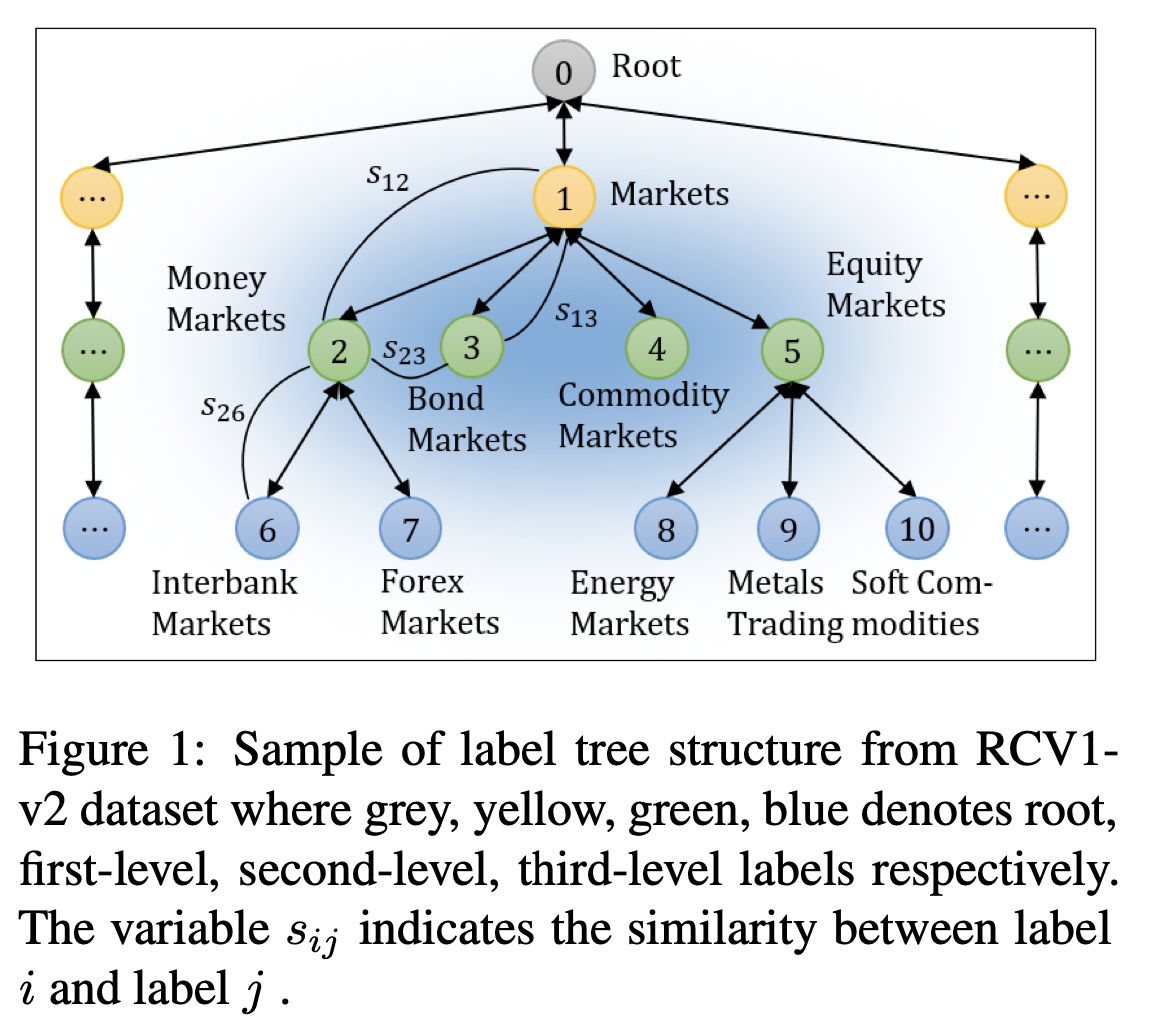
例如上图中的\(s_{23}\)就是区别信息(同层节点之间),\(s_{26}\)表示相关信息(父子节点之间)。
Method
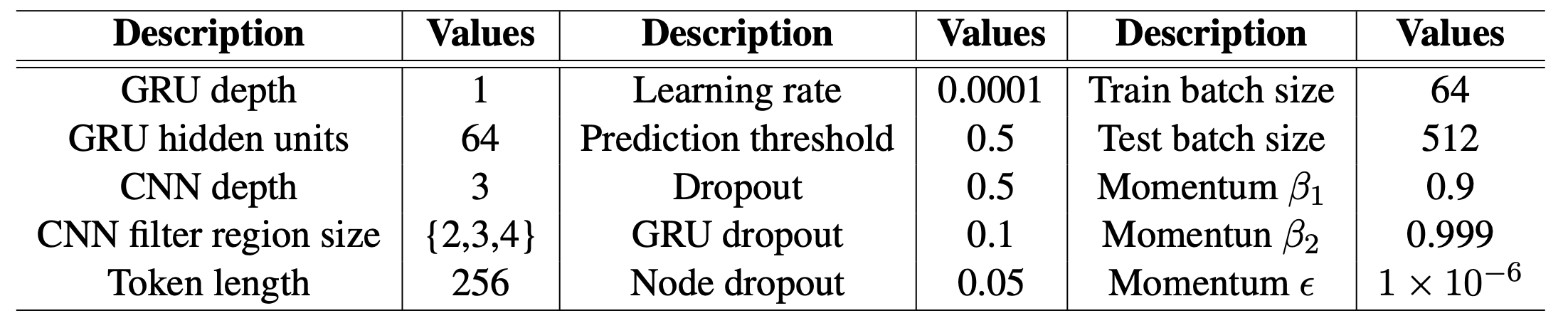
本文选用了Bi-GRU作为文本编码器,采用CNN提取N-Gram特征。对于文本\(T=\{x_1,x_2,\cdots,x_n\}\),卷积核输出特征\(O=\{P^1,P^2,\cdots,P^K\}\)。
之后接一个线性Transformer(全连接层) \[ V=Reshape(MO) \] 其中\(M\in\mathbb{R}^{d_w\times d_c}\),\(O\in\mathbb{R}^{d_c}\)为文本特征,\(V\in\mathbb{R}^{m\times d_n}\)。
本文采用了HiAGM中的Hierarchy-GCN框架,节点可以聚合父子节点的信息。对于\(\mathcal{G}=(\mathcal{V},\mathcal{E})\),\(v_k\in\mathbb{R}^{d_n}\)表示节点k的特征,\(N(k)=\{n_k,child(k),parent(k)\}\)表示节点的邻居。节点k的隐层状态通过下式计算: \[ \begin{align} a_{j,k} &= \left|\frac{v_j\cdot v_k}{\lVert v_j\rVert\cdot \lVert v_k\rVert}\right|, \\ \mu_{j,k} &= a_{j,k}v_j + b_l^k, \\ g_{j,k} &= \sigma(W_g^{d(j,k)}v_j+b_g^k), \\ h_k &= ReLU(\sum_{j\in N(k)}g_{j,k}\cdot \mu_{j,k}) \end{align} \] 其中\(W_g^{d(j,k)}\in\mathbb{R}^n\)表示节点j到节点k的门控权重。
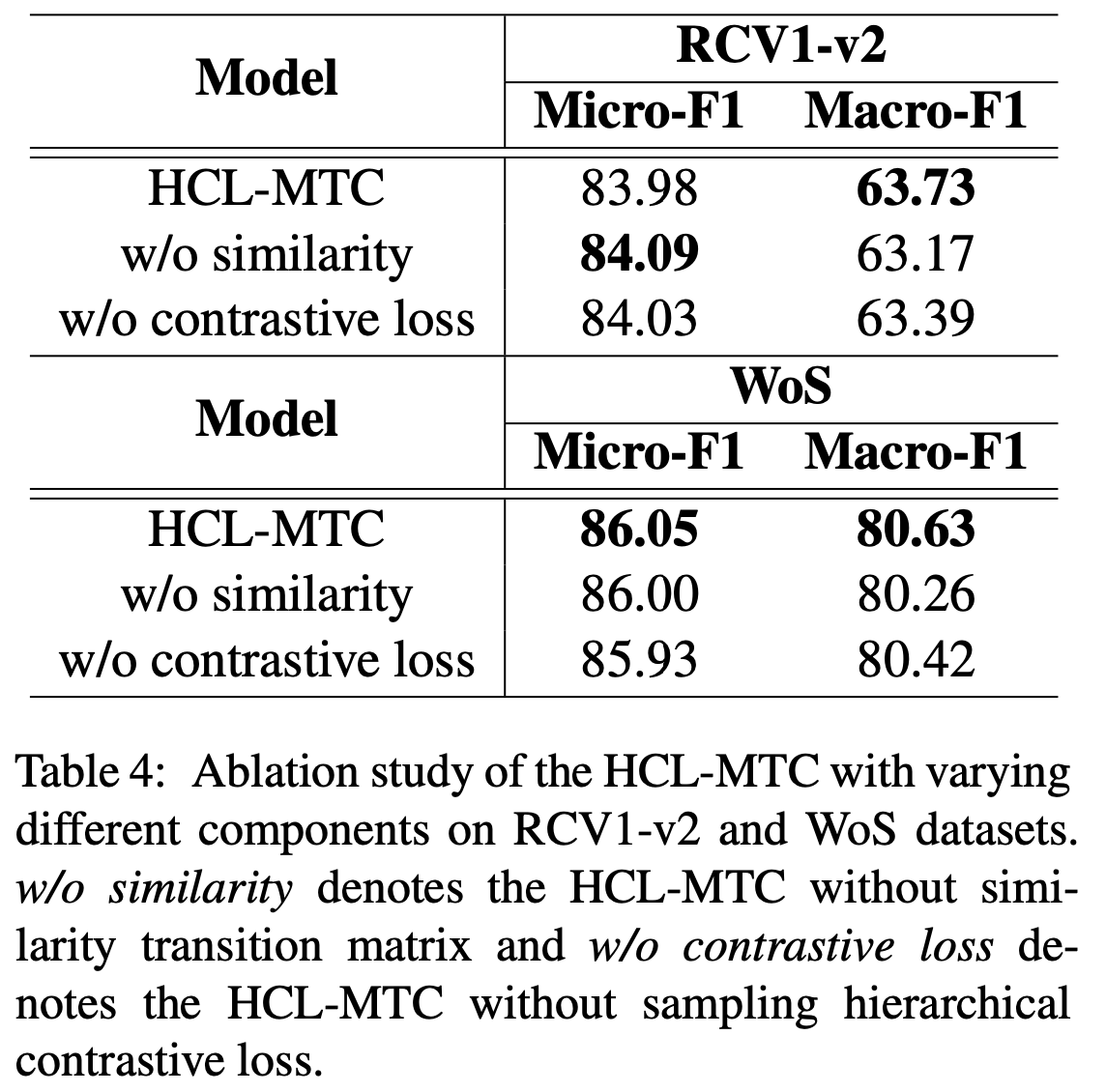
作者定义了采样层次对比损失(Sampling Hierarchical Contrastive Loss),用\(s(v_{p_i}, v_{p_j})\)表示父节点之间的相似度,用\(s(v_{p_i}, v_{c_k})\)表示父子节点的相似度。
在标签树中,父子标签对能够双向传递信息,但父节点之间不能传递信息。从而优化目标是最大化区别信息\(s(v_{p_i}, v_{p_j})\),最小化相关信息\(s(v_{p_i}, v_{c_k})\),损失函数定义如下 \[ \begin{align} &s(v_{p_i}, v_{p_j}) = \left|\frac{v_{p_i}\cdot v_{p_j}}{\lVert v_{p_i}\rVert\cdot \lVert v_{p_j}\rVert}\right| \\ &s(v_{p_i}, v_{c_k}) = \left|\frac{v_{p_i}\cdot v_{c_k}}{\lVert v_{p_i}\rVert\cdot \lVert v_{c_k}\rVert}\right| \\ &L_d = \sum_{p_i\in\mathcal{V}}\sum_{p_j\in\mathcal{V}}\sum_{c_k\in child(i)}\exp(s(v_{p_i}, v_{p_j}) - s(v_{p_i}, v_{c_k})) \end{align} \] 因为枚举所有节点对时间代价大,为此需要采样,每一层只随机选取两个父节点和一个子节点参与计算。
最终的损失函数是BCE、递归正则化损失和采样层次距离损失的加权。
Recursive Regularization for Large-scale Classification with Hierarchical and Graphical Dependencies, KDD 2013 [paper]
\[ \begin{align} L_c &= -\sum_{i=1}^m[y_i\log(y_i')+(1-y_i)\log(1-y_i')] \\ L_r &= \sum_{i\in\mathcal{V}}\sum_{j\in child(i)}\frac12\lVert w_i-w_j\rVert^2 \\ L &= L_c + \lambda_1L_r + \lambda_2L_d \end{align} \]
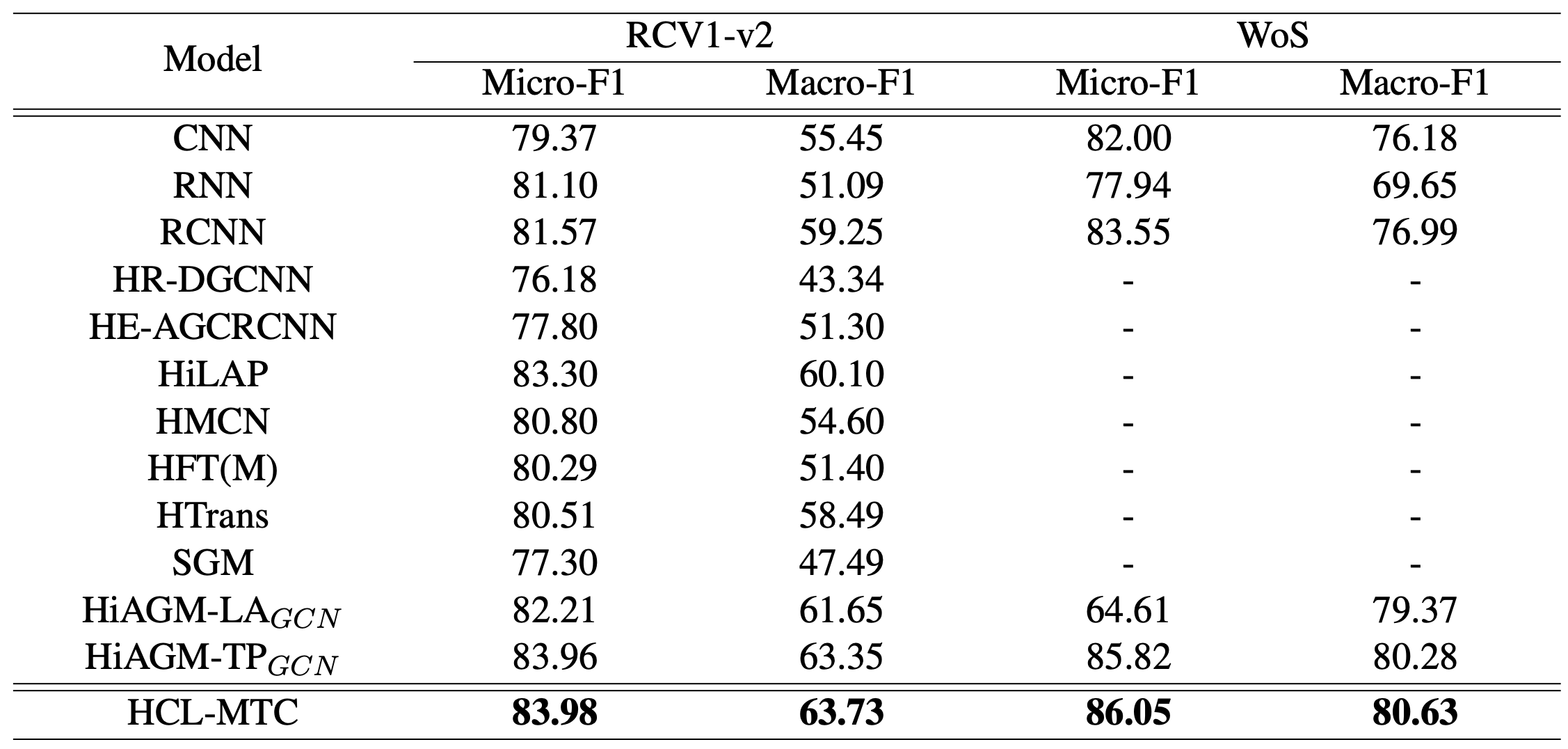
Experiment
选择RCV1-V2和WoS数据集。