Balancing Methods for Multi-label Text Classification with Long-Tailed Class Distribution
EMNLP 2021,损失函数大杂烩。
Overview

- paper: https://aclanthology.org/2021.emnlp-main.643.pdf
- code: https://github.com/Roche/BalancedLossNLP
Background
多标签分类通常面对长尾分布的问题,只有一小部分标签频繁出现,大部分标签的样本都很少。
本文介绍了多标签分类中的一些平衡损失函数,在Reuters-21578和PubMed上进行了实验。
Method
Binary Cross Entropy (BCE)
BCE是最基础的损失函数,其中\(p_i^k = \sigma(z_i^k)\)。 \[ L_{BCE} = \begin{cases} -\log(p_i^k) & \text{if}\ y_i^k = 1 \\ -\log(1-p_i^k) & \text{otherwise} \end{cases} \]
Focal Loss (FL)
Focal Loss由恺明大神提出,在更难分类的样本上增加了损失权重。 \[ L_{FL} = \begin{cases} -(1-p_i^k)^\gamma\log(p_i^k) & \text{if}\ y_i^k = 1 \\ -(p_i^k)^\gamma\log(1-p_i^k) & \text{otherwise} \end{cases} \]
Class-Balanced focal loss (CB)
类别平衡的损失函数对Focal Loss进一步加权,以捕获数据的边际递减效应,减少了头部样本的冗余信息。
对于每个标签,出现频率为\(n_i\),则有平衡项 \[ r_{CB} = \frac{1-\beta}{1-\beta^{n_i}} \] 其中\(\beta\in[0,1)\),控制了有效样本的增长速度。 \[ L_{FL} = \begin{cases} -r_{CB}(1-p_i^k)^\gamma\log(p_i^k) & \text{if}\ y_i^k = 1 \\ -r_{CB}(p_i^k)^\gamma\log(1-p_i^k) & \text{otherwise} \end{cases} \]
Distribution-Balanced loss (DB)
通过整合再平衡权重以及negative tolerant regularization(NTR),分布平衡函数减少了标签共现的冗余信息,并且对“容易分类的”样本分配较低的权重
首先,为了重新平衡权重,在单标签的情况下,一个样本可以通过重采样概率\(P_i^C=\frac1C\frac1{n_i}\) 来加权,但是在多标签的情况下,如果采用同样的策略\(P^I = \frac1C\sum_{y_i^k}\frac1{n_i}\),样本会被过采样。
因此,需要引入权重归一化\(r_{DB} = P_i^C/P^I\),可以采用平滑函数\(\hat{r}_{DB} = \alpha+\sigma(\beta\times(r_{DB}-\mu))\),将\(r_{DB}\)映射到区间\([\alpha,\alpha+1]\),从而重平衡的Focal Loss定义如下。 \[ L_{R-FL} = \begin{cases} -\hat{r}_{DB}(1-p_i^k)^\gamma\log(p_i^k) & \text{if}\ y_i^k = 1 \\ -\hat{r}_{DB}(p_i^k)^\gamma\log(1-p_i^k) & \text{otherwise} \end{cases} \] NTR机制将正负样本区别对待,引入了一个缩放因子\(\lambda\)和一个内在的类别偏差,以降低尾部类别的门限,避免过度抑制。 \[ L_{NTR-FL} = \begin{cases} -(1-q_i^k)^\gamma\log(q_i^k) & \text{if}\ y_i^k = 1 \\ -\frac1\lambda(q_i^k)^\gamma\log(1-q_i^k) & \text{otherwise} \end{cases} \] 其中对于正例\(q_i^k=\sigma(z_i^k-v_i)\),对于负例\(q_i^k=\sigma(\lambda(z_i^k-v_i))\)。\(v_i\)可以在训练开始时最小化损失函数估计,缩放因子为\(\kappa\),类别先验为\(p_i=n_i/N\)。 \[ \hat{b}_i = -\log(\frac1{p_i}-1),v_i=-\kappa\times\hat{b}_i \] 从而最终的损失函数为 \[ L_{DB} = \begin{cases} -\hat{r}_{DB}(1-q_i^k)^\gamma\log(q_i^k) & \text{if}\ y_i^k = 1 \\ -\hat{r}_{DB}\frac1\lambda(q_i^k)^\gamma\log(1-q_i^k) & \text{otherwise} \end{cases} \]
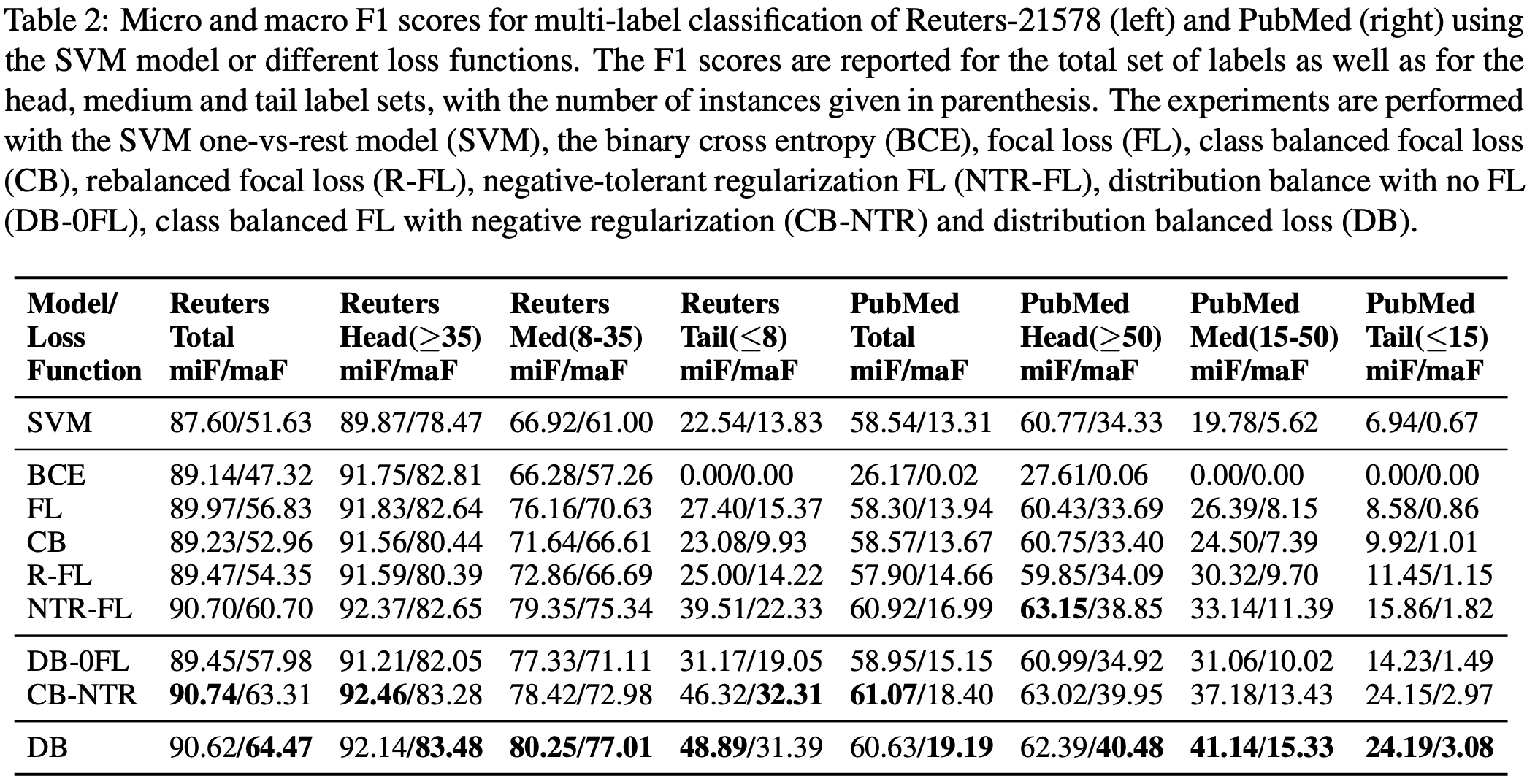
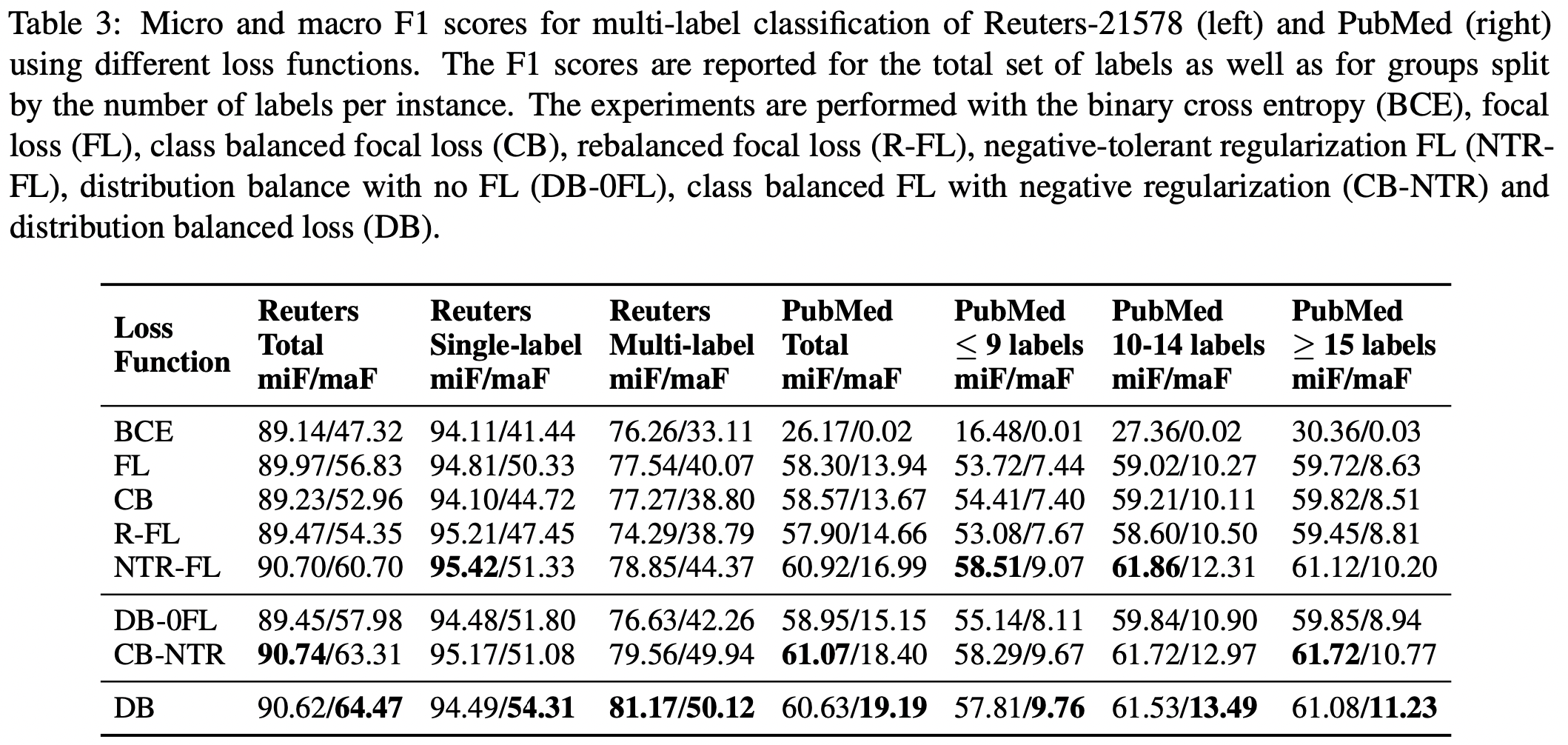
Experiment
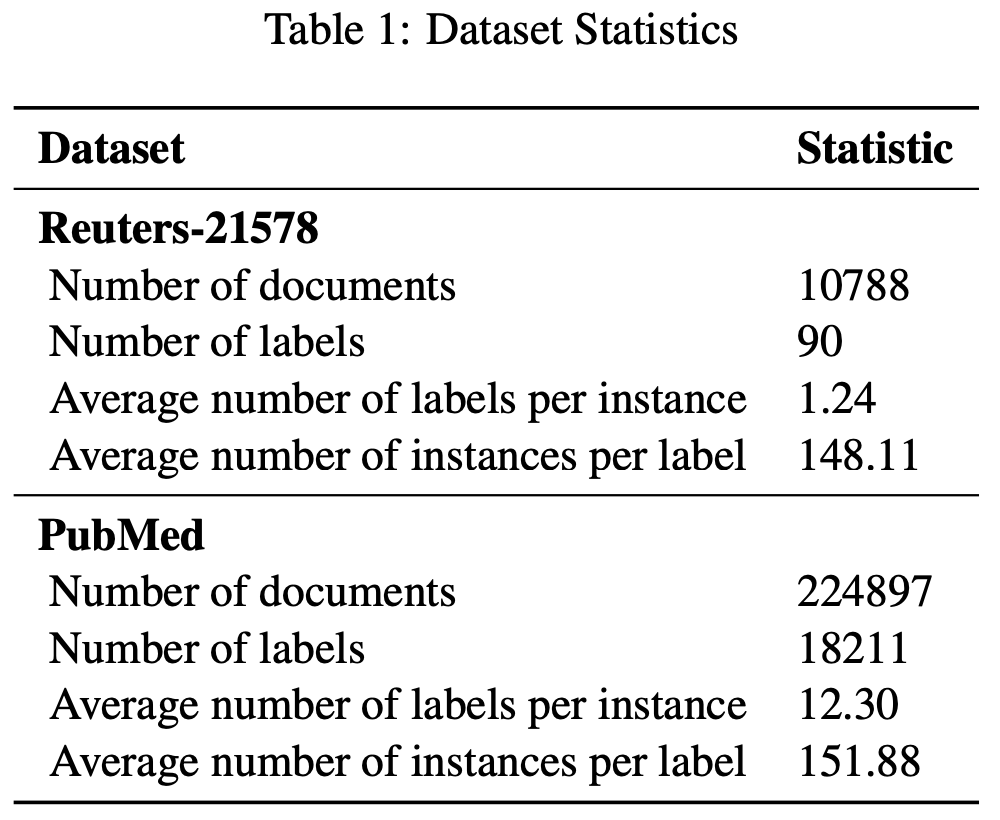
选取Reuters-21578和PubMed数据集,采用SVM(???)作为baseline。
直接使用了transformers中的BertForSequenceClassification,Reuters-21578选用了bert-base-cased,PubMed使用了biobert-base-cased。最大长度512,batch size为32。