Enhancing Label Correlation Feedback in Multi-Label Text Classification via Multi-Task Learning
ACL Findings 2021,使用多任务学习加强标签相关性的反馈,设计了标签对共现预测(Pairwise Label Co-occurrence Prediction, PLCP)和条件标签共现预测(Conditional Label Co-occurrence Prediction, CLCP)两个任务。
Overview

- paper: https://arxiv.org/pdf/2106.03103.pdf
- code (tensorflow): https://github.com/EiraZhang/LACO
- dataset: RCV1-V2 AAPD
Background
在多标签文本文类任务中,利用标签相关性的模型可以更好地泛化,有利于建模低频标签。基于Seq2Seq的方法可以有效捕获标签相关性,但也有几点不足:
- 依赖预先定义的标签顺序,模型对此十分敏感。
- 容易在训练集上过拟合,难以泛化至没有见过的标签组合。
- 存在错误传播的问题。
本文采用多任务学习的框架,基于Transformer引入joint embedding机制。通过self-attention和cross-attention,将文本信息和标签信息深度交互。并设计两个标签共现的预测任务,用于捕获标签之间的相关性。
- 标签对共现预测PLCP:通过两两组合,判断标签是否相关,捕获二阶相关性。
- 条件标签共现预测CLCP:给定部分相关标签集合,预测其他位置标签的相关性,可以捕获高阶相关性。
除去多任务的部分,模型结构和CORE一致。
Correlation-Guided Representation for Multi-Label Text Classification, IJCAI 2021. [paper]
Method
Document-Label Joint Embedding (JE)
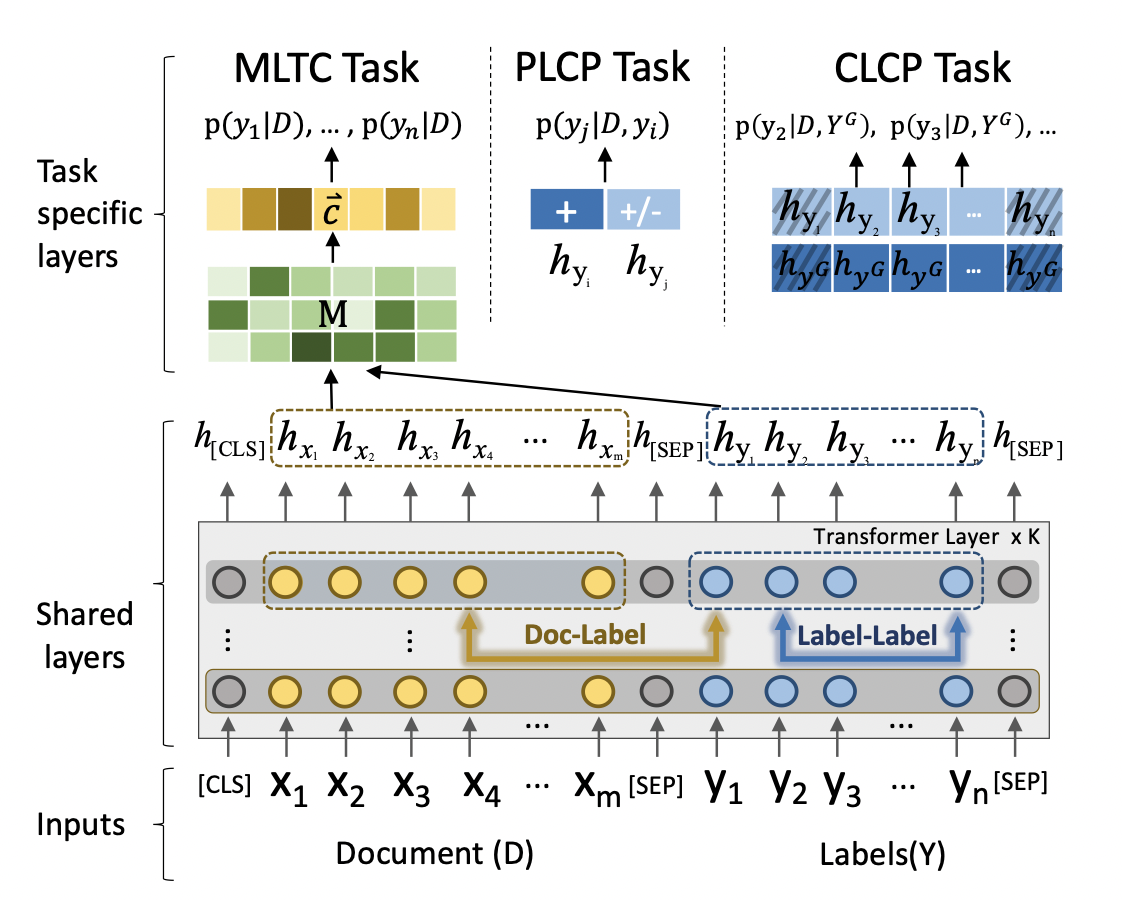
将文本序列和标签序列通过[SEP]拼接作为输入序列,表示为\(\{[CLS],x_1,\cdots,x_m,[SEP],y_1,\cdots,y_n,[SEP]\}\),进入BERT后得到隐层表示\(\{h_{[CLS]},h_{x_1},\cdots,h_{x_m},h_{[SEP]},h_{y_1},\cdots,h_{y_n},h_{[SEP]}\}\)。
联合embedding的方式既兼顾了文本与标签的相关性,也考虑到了标签内部的相关性(但这种方法在标签数目过多时显然不适用)。
作者还显式地引入了cross-attention计算,称为Document-Label Cross Attention: \[ M = H_DH_Y^T \] 其中\(H_D = [h_{x_1},\cdots,h_{x_m}]\)为文本序列的embedding,\(H_Y=[h_{y_1},\cdots,h_{y_n}]\)为标签序列的embedding,\(M\in\mathbb{R}^{m\times n}\)。对于长为\(2r+1\)的文本,\(M_{i-r;i+r}\)衡量了标签-短语对的相关性。
为了提升稀疏正则化的有效性(???),作者还使用了CNN,结合max-pooling得到最终的文本表示\(\vec{c}\)。 \[ \vec{c} = \Omega(M_{i-r;i+r})·H_D \] 对文本表示接全连接层得到预测结果,采用BCE损失函数即可。
PLCP Task
作者将标签集分为\(Y^+\)和\(Y^-\)两类,\(Y^+\)表示相关的标签(共同出现过),\(Y^-\)表示不相关的标签。
标签对一部分从\(Y^+\)中挑选,标记为IsCo-occur,另一部分从\(Y^+\)和\(Y^-\)中挑选,标记为NotCo-occur,比例设为\(\gamma\)。将两个标签的embedding拼接\([y_i, y_j]\)作为输入,采用交叉熵计算损失。 \[ \mathcal{L}_{plcp} = -[q_{ij}\ln p_{ij} + (1-q_{ij})\ln(1-p_{ij})] \]
构造标签集
label_list = example.label.split(" ")
label_ids = _predicate_label_to_id(label_list, label_map)
right_labels = []
wrong_labels = []
for label_id in range(0,len(label_ids)):
if label_ids[label_id]==1:
right_labels.append(label_id)
else:
wrong_labels.append(label_id)
right_pair = list(itertools.combinations(right_labels, 2))
contrast_dict = {}
for pair in right_pair:
contrast_dict[pair]=[0,1]
for i in range(0,int(len(right_pair)*2)):
r = random.sample(right_labels,1)[0]
w =random.sample(wrong_labels,1)[0]
contrast_dict[(r,w)]=[1,0]构造feature并采样
feature_list=[]
for pair in contrast_dict.keys():
feature = InputFeatures(
input_ids=input_ids,
input_mask=input_mask,
segment_ids=segment_ids,
token_label_ids=token_label_ids,
label_ids=label_ids,
fit_labelspace_positions=fit_labelspace_positions,
fit_docspace_positions=fit_docspace_positions,
pair = list(pair),
pair_target=list(contrast_dict[pair]),
# pair = list([0,1]),
# pair_target= list([0,1]),
is_real_example=True)
feature_list.append(feature)
a = random.sample(feature_list, 1)CLCP Task
从\(Y^+\)中随机采样\(s\)个标签,形成\(Y^G\),然后判断剩余的标签是否与其相关。为此引入了一个额外的位置向量\(E_Y = [e_{y_1},\cdots,e_{y_n}]\),\(e_{y_i}=0\)就表示标签被采样了,也即\(y_i\in Y^G\),反之则\(y_i\in Y-Y^G\)。
将所有被采样的标签表示做平均得到\(h_{y^G}\),将其拼接到所有未被采样的标签表示,作为输入特征。同样采用交叉熵作为损失函数。 \[ \mathcal{L}_{clcp} = -\sum_{i=1}^{n-s}[q_{i}\ln p_{i} + (1-q_{i})\ln(1-p_{i})] \] 其中\(q_i\in\{0,1\}\)表示标签\(y_i\)是否与\(Y^G\)中的标签共同出现。
right_mask_labels = random.sample(right_labels,1)
for num_label in range(0,54) :
if num_label not in right_mask_labels:
fit_labelspace_mask_positions.append(num_label)
else:
fit_labelspace_given_positions.append(num_label)
for mask_position in fit_labelspace_mask_positions:
if mask_position in right_labels:
mask_lm_ids.append(1)
else:
mask_lm_ids.append(0)Experiment
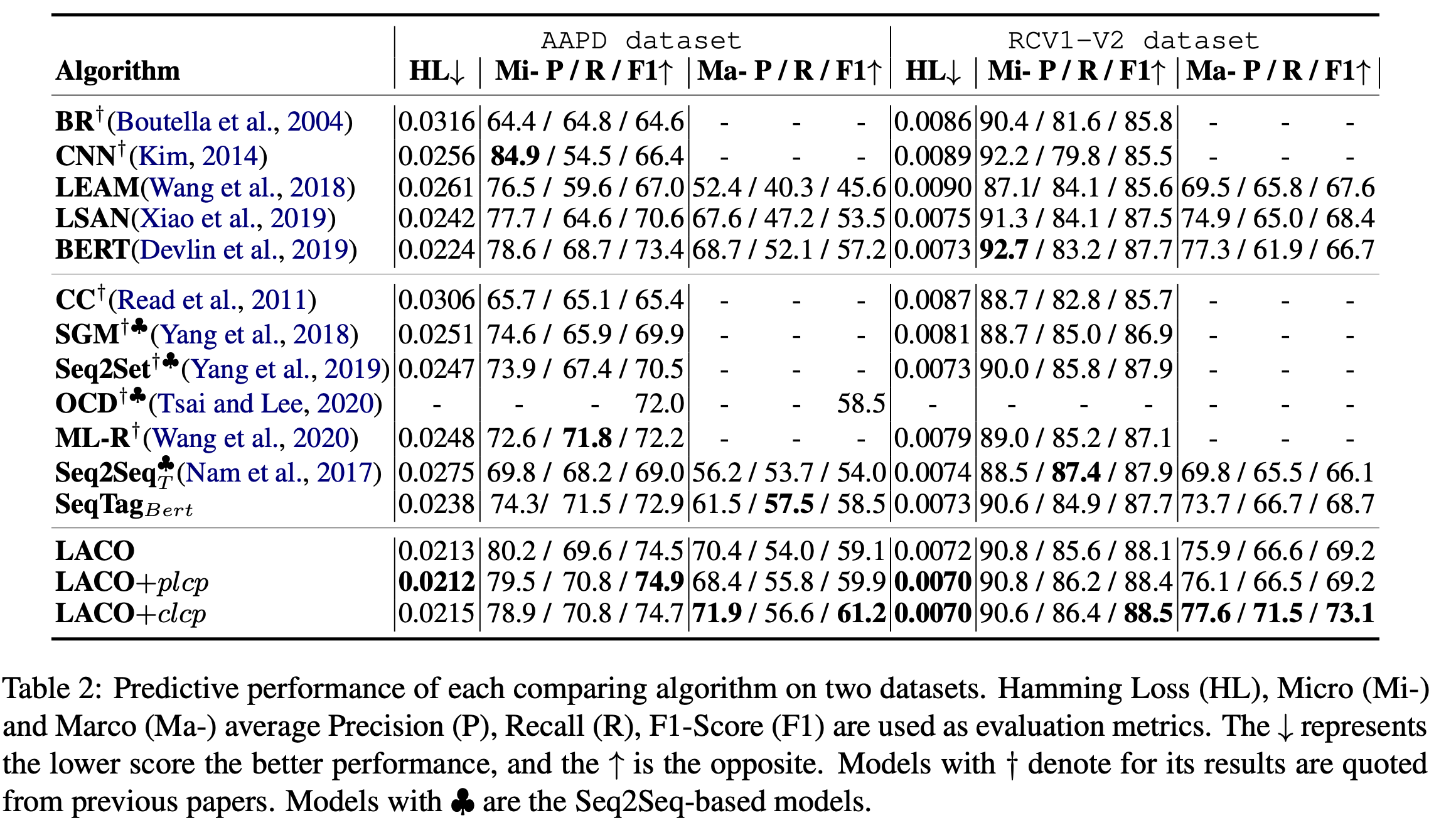
在AAPD和RCV1-V2上进行了实验,实验设置为bert-base-uncased,batch size为32,最大长度320,学习率为5e-5,\(\gamma\)为0.5。
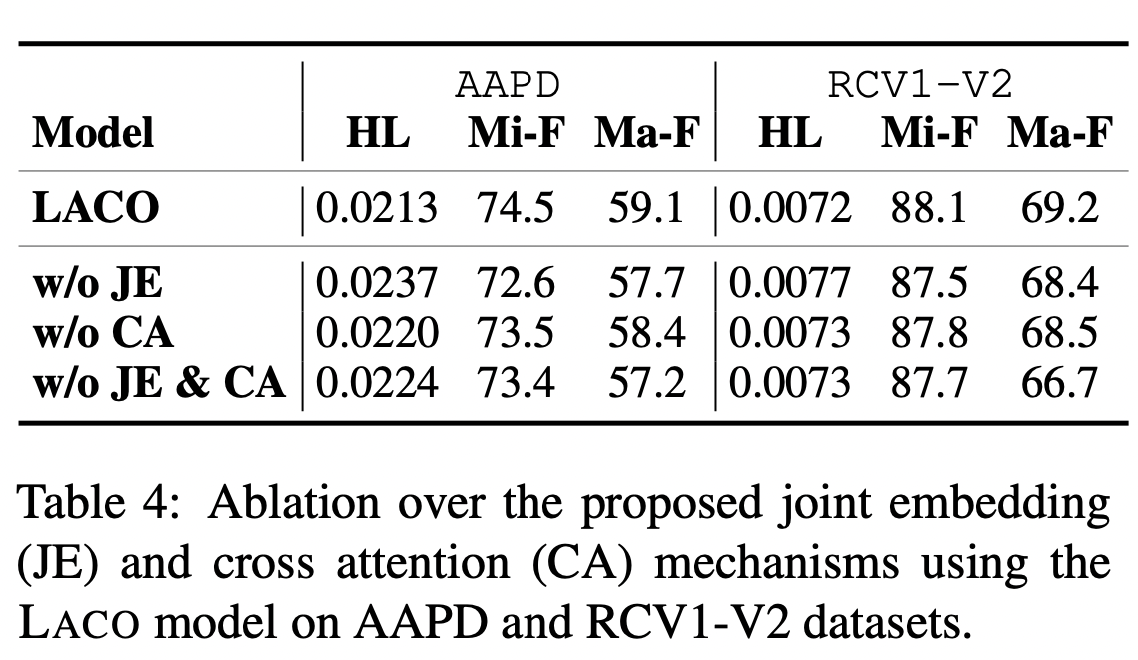
Ablation
LACO在低频标签上能够取得更好的性能(提高召回,但准确率可能下降?)。
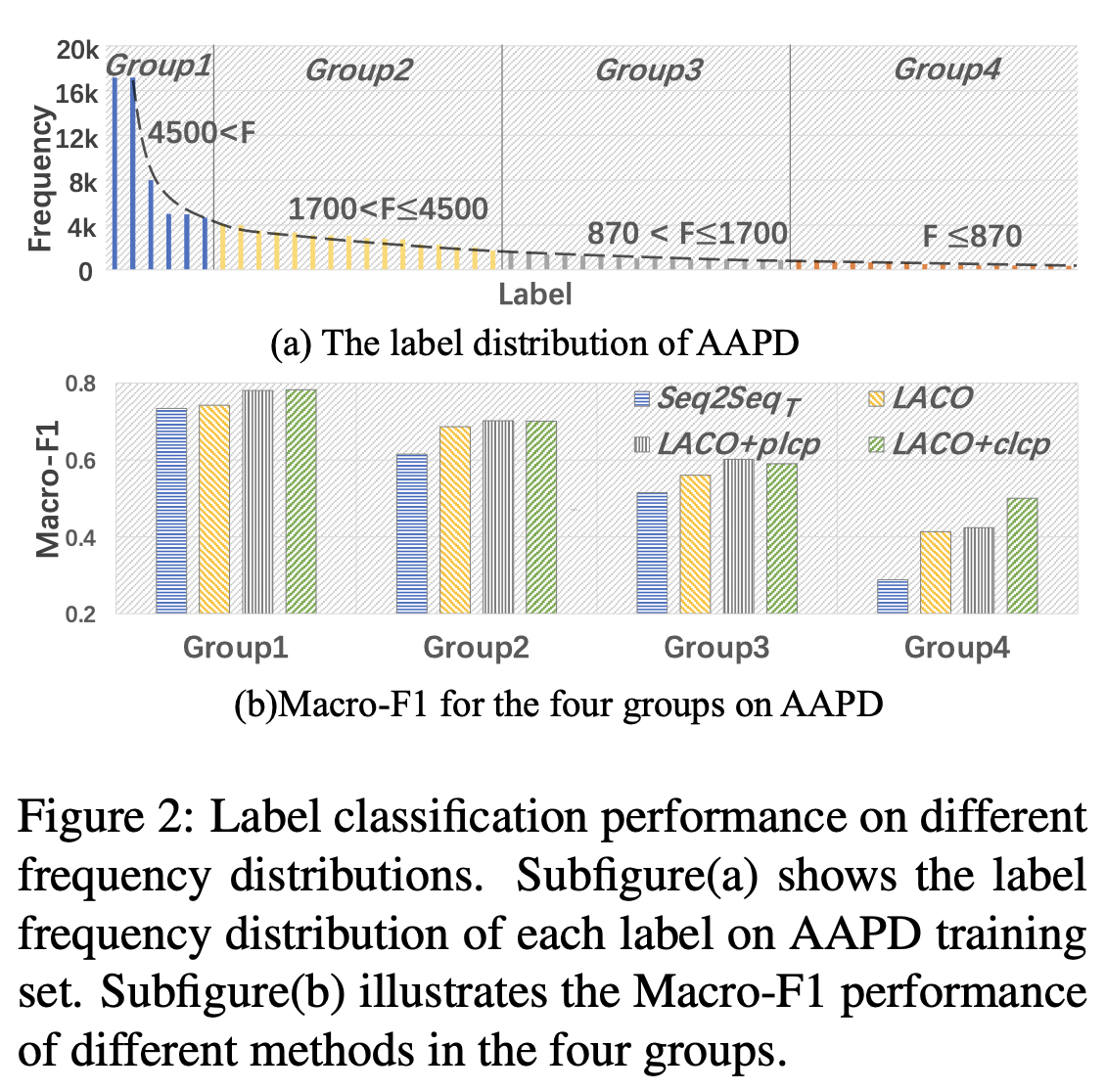
LACO预测出了更多样的标签组合。
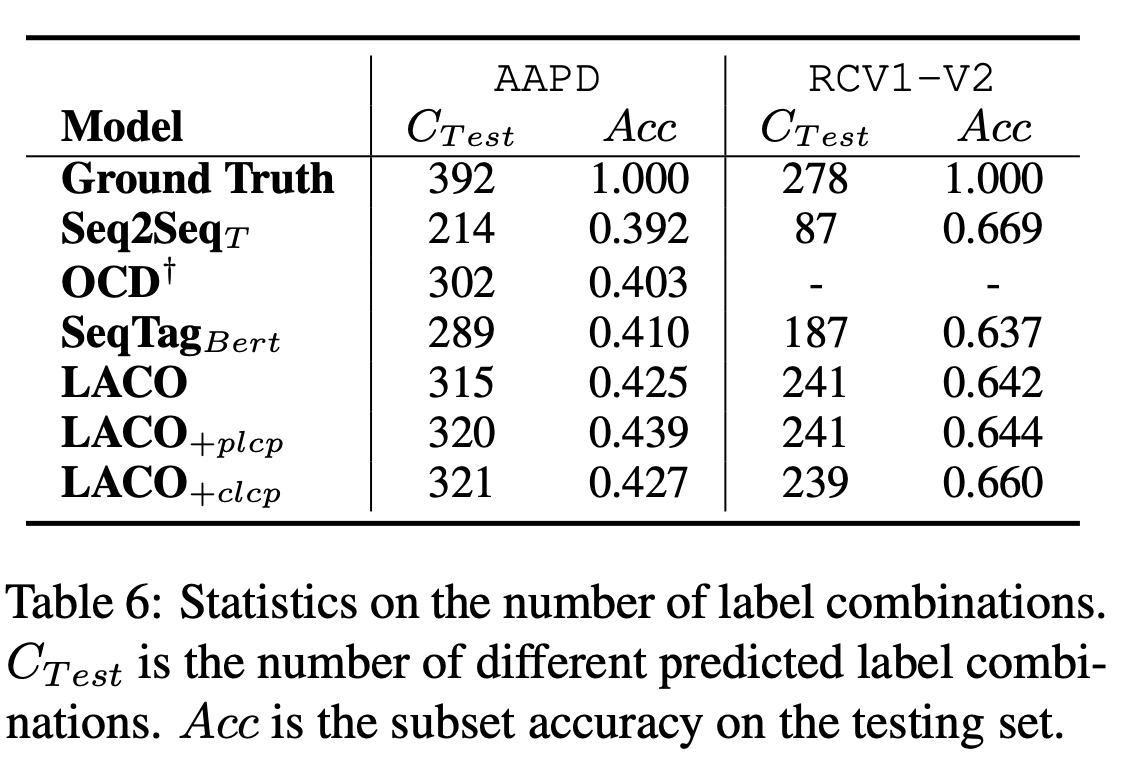
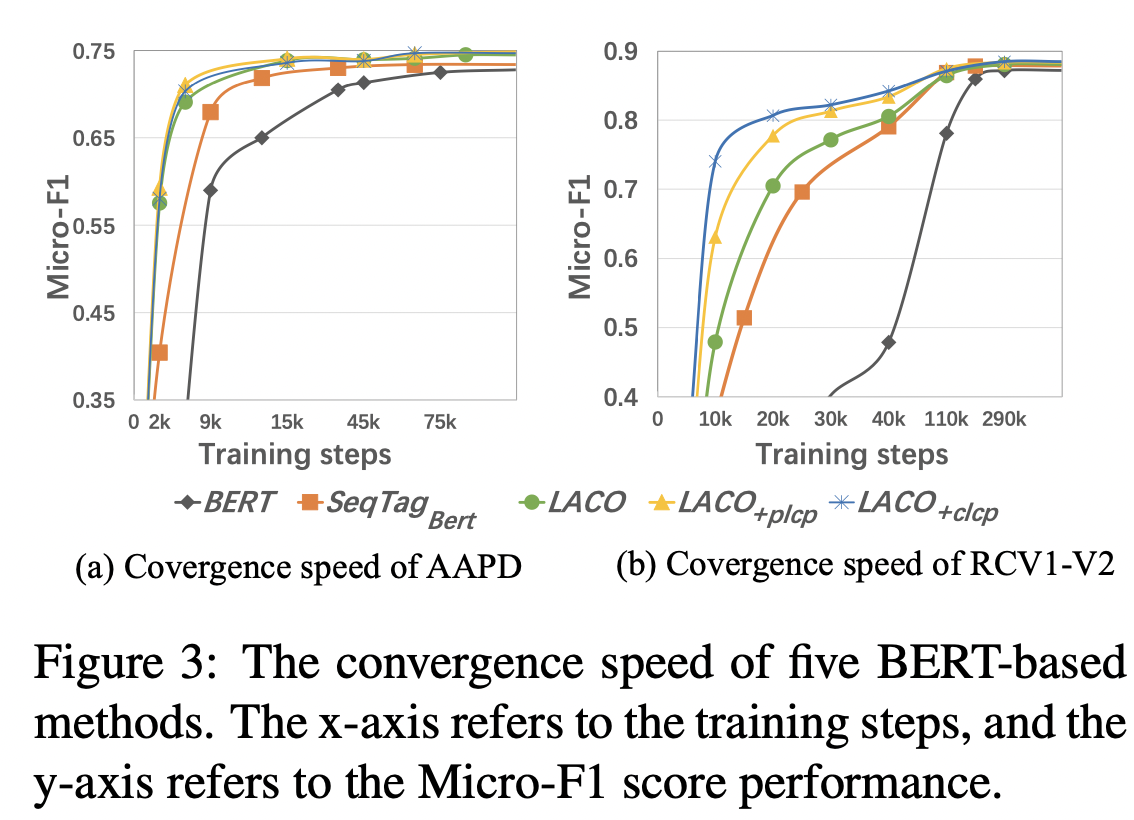
LACO相比于BERT类模型,得益于多任务之间的特征交互,可以获得更快的收敛速度。