Graph Neural Networks with Learnable Structural and Positional Representations
来自Bengio组,在GNN上引入位置编码,提出了一种新的框架LSPE,在分子数据集上的性能提升了2.87%至64.14%。
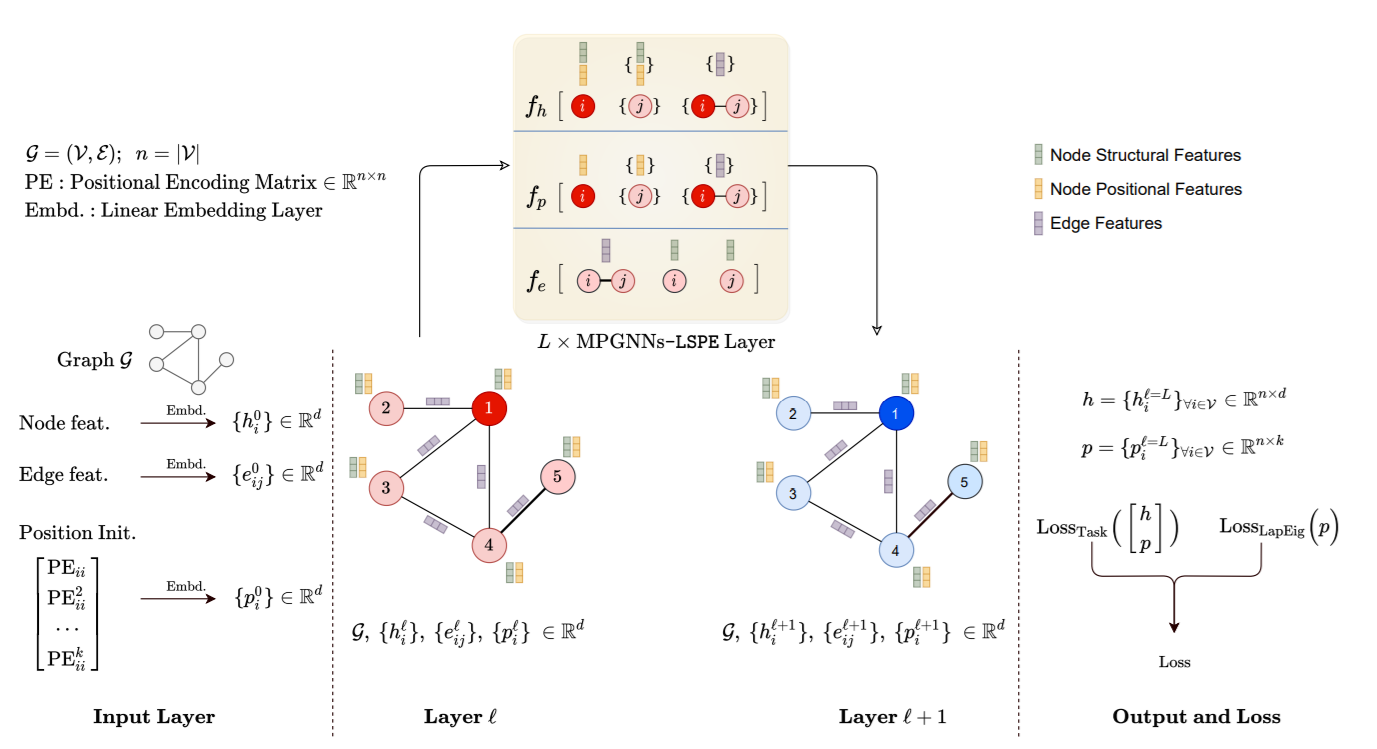
Overview

arxiv: https://arxiv.org/pdf/2110.07875v1.pdf
code: https://github.com/vijaydwivedi75/gnn-lspe
Background
GNN大多是基于消息传递机制,通过聚合邻居的信息构建节点表示,但这也带来了一定的局限性。每个节点的表示只依赖于一小块local结构,而没有考虑到节点的位置信息。比如图中两个节点有着相同的1-hop邻居,但2-hop或高阶邻居都不甚相同,此时GNN不能区分两个节点。面对这种局限性,可以有三种方法:
堆叠多层网络,因为过平滑现象可能难以适用长距离的节点;
采用高阶的GNN,增加了计算代价;
考虑节点的位置编码。
本文希望设计一种可学习的位置编码与GNN结合,从而可以提升GNN的节点表示能力,同时保持线性的计算复杂度便于大规模应用。
Method
Notation
假设图为\(\mathcal{G} = (\mathcal(V), \mathcal{E})\),其中\(n = \lvert \mathcal{V} \rvert\)表示节点数,\(E=\lvert \mathcal{E} \rvert\)表示边数。\(A\in\mathbb{R}^{n\times n}\)为邻接矩阵,\(A_{ij} = 1\)表示两个节点有边相连,否则\(A_{ij} = 0\),\(D\in\mathbb{R}^{n\times n}\)表示节点的度矩阵。\(h_i\)和\(p_i\)分别表示节点\(i\)的表示和位置编码,\(e_{ij}\)表示节点\(i\)和节点\(j\)相连的边的特征。
GNN模型一般有三个主要部分:嵌入层、堆叠的卷积层以及最后基于任务的层,用上标\(l\)表示层数,标准的MP-GNN参数更新公式如下: \[ \begin{align} \text{MP-GNNs}: \quad h_i^{l+1} &= f_h(h_i^{l}, \{h_j^{l}\}_{j\in\mathcal{N}_i}, e_{ij}^l), \ h_i^{l+1}, h_i^{l}\in \mathbb{R}^d, \tag{1} \label{eq1}\\ e_{ij}^{l+1} &= f_e(h_i^{l}, h_j^{l}, e_{ij}^l), \ e_{ij}^{l+1}, e_{ij}^{l}\in \mathbb{R}^d \tag{2} \end{align} \]
其中\(f_h\)和\(f_e\)表示有可学习参数的函数,\(\mathcal{N}_i\)表示节点\(i\)的邻居。Transformer也被认为是MP-GNNs的一种特例,考虑全连通图,将\(\eqref{eq1}\)中的边特征丢弃,简化形式即为Transformer。
Positional Encoding
现有MP-GNN中融合位置信息往往是通过拼接的方式: \[ \begin{align} h_i^{\mathcal{l}=0} &= \mathrm{LL}_h{ \begin{bmatrix} {h_i^{\mathrm{in}} \\ p_i^{in}} \end{bmatrix}} = D^0{ \begin{bmatrix} {h_i^{\mathrm{in}} \\ p_i^{in}} \end{bmatrix}} +d^0\in\mathbb{R}^d,\tag{3} \\ e_{ij}^{l=0} &= \mathrm{LL}(e_{ij}^{\mathrm{in}}) = B^0e_{ij}^{\mathrm{in}}+b^0\in\mathbb{R}^d \tag{4} \end{align} \] 其中\(p_i^\mathrm{in}\in\mathbb{R}^k\)表示输入节点的位置编码,\(D^0\in\mathbb{R}^{d\times(d_v+k)}\)和\(d_0\in\mathbb{R}^d\)表示全连接层的参数。这种方法融合了位置表示和结构化表示,同时保持了线性的计算复杂度,但是不能动态改变位置表示以更好地适应当前任务。
针对上述问题,本文将位置信息与结构信息分离,两种表示可以分别学习,这种框架称为可学习的结构和位置编码(Learnable Structural and Positional Encodings,LSPE)。 \[ \begin{align} \text{MP-GNNs-LSPE}: \quad h_i^{l+1} &= f_h\left( \begin{bmatrix} h_i^{l} \\ p_i^l \end{bmatrix}, \left\{ \begin{bmatrix} h_i^{l}\\p_i^l \end{bmatrix} \right\}_{j\in\mathcal{N}_i}, e_{ij}^l\right), \ h_i^{l+1}, h_i^{l}\in \mathbb{R}^d, \tag{5} \label{eq2} \\ e_{ij}^{l+1} &= f_e(h_i^{l}, h_j^{l}, e_{ij}^l), \ e_{ij}^{l+1}, e_{ij}^{l}\in \mathbb{R}^d \tag{6} \\ p_i^{l+1} &= f_p(p_i^l, \{p_j^{l}\}_{j\in\mathcal{N}_i}, e_{ij}^l),\ p_i^{l+1},p_i^l\in\mathbb{R}^d, \tag{7} \end{align} \]
Definition of Initial PE
初始位置编码的选择很重要,本文比较了两种编码:Laplacian PE(LapPE)和Random Walk PE(RWPE)。LapPE为每个节点提供了唯一表示,并且是距离敏感的,但是受限于符号不明确,在训练过程中需要随机翻转符号。
本文提出了RWPE编码,定义如下: \[ p_i^{\mathrm{RWPE}} = [\mathrm{RW}_{ii}, \mathrm{RW}_{ii}^2, \cdots,\mathrm{RW}_{ii}^k]\in\mathbb{R}^k\tag{8} \] 其中\(\mathrm{RW}=AD^{-1}\),本文没有使用完整的随机游走矩阵\({R_{ij}}\),而是只考虑了节点自身的随机游走矩阵,降低了计算复杂度。RWPE编码没有LapPE的符号不明确问题,不需要随机额外的invariance,同时也提供了唯一的节点表示,在节点有一个独特的k-hop拓扑邻居时。
Positional Loss
因为本文分离了位置信息,因此可以考虑设计位置编码loss以强迫其学习图的拓扑结构,本文采用的是Laplacian eigenvector loss。 \[ \begin{align} \text{Loss} &= \text{Loss}_{\text{Task}}\left( \begin{bmatrix} h^{l=L} \\ p^{l=L} \end{bmatrix} \right) + \alpha\ \text{Loss}_{\text{LapEig}}(p^{l=L}) \tag{9} \\ \text{Loss}_{\text{LapEig}}(p) &= \frac{1}{k}\text{trace}(p^T\Delta p) + \frac{\lambda}{k} \lVert p^Tp-\mathrm{I}_k \rVert^2_F \tag{10} \end{align} \] 其中\(h^{l=L}\in\mathbb{R}^{n\times d}\),\(p^{l=L}\in\mathbb{R}^{n\times k}\),\(\lVert \cdot \rVert_F\)表示Frobenius范数,定义为矩阵各项元素平方和的平方根。此外注意到,本文限制位置向量的均值为0范数为1,以更好地近似Laplacian eigenvector loss。
Experiment
在三个数据集ZINC、OGBG-MOLTOX21和OGBG-MOLPCBA上进行了实验,在不使用PE时图网络很难取得好的表现。
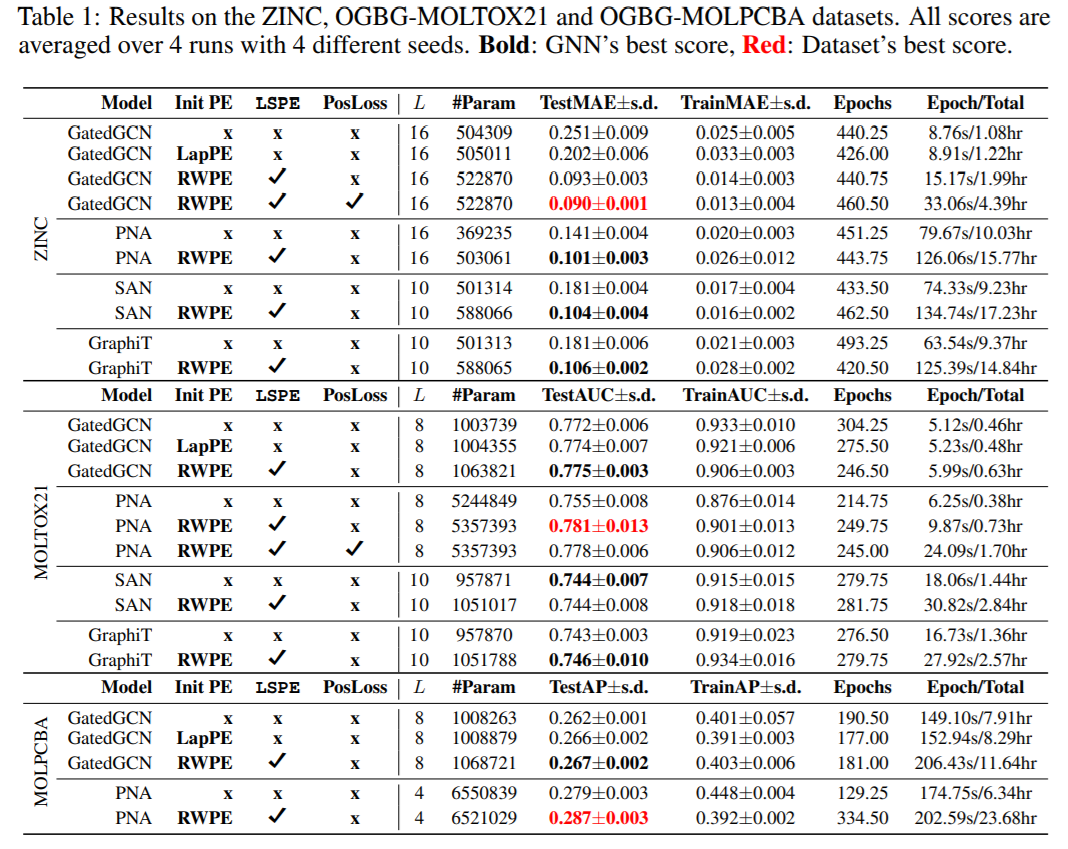
本文也比较了稀疏GNN和Transformer GNN类的方法,稀疏GNN在LSPE的加持下取得了更好的结果,尽管Transformer GNN理论上可以更好地克服长距依赖的局限性。
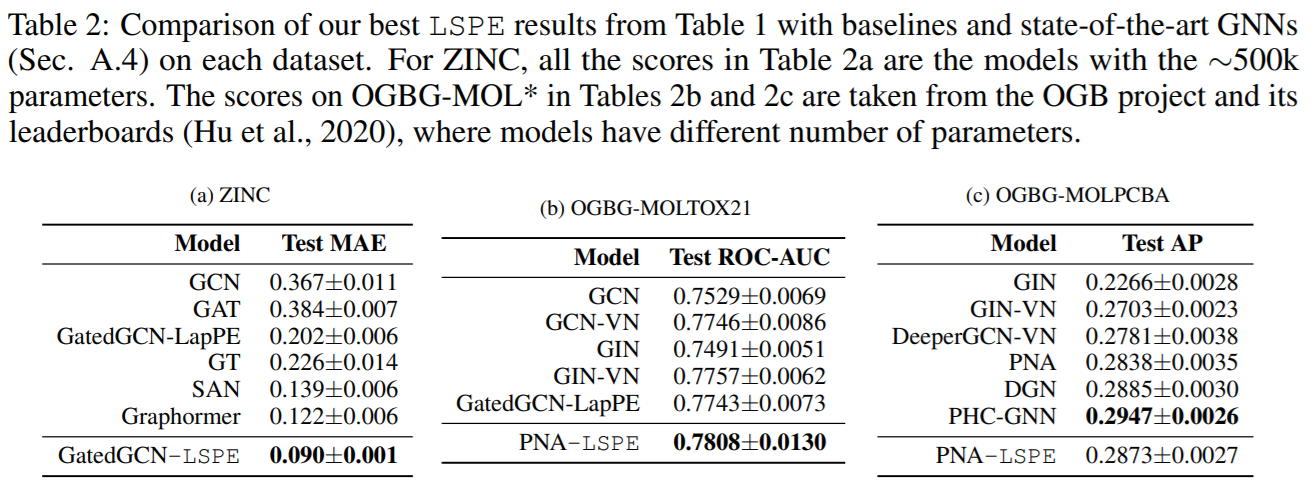
此外,本文对k的选择也做了实验,结果上来看适当大一点比较好。