现代密码学(三)分组密码
介绍分组密码,包括Feistel Cipher、DES和IDEA等。
分组密码
分组密码(Block Cipher),是指将明文分成许多块,利用加密算法对每一块进行加密,形式如下。
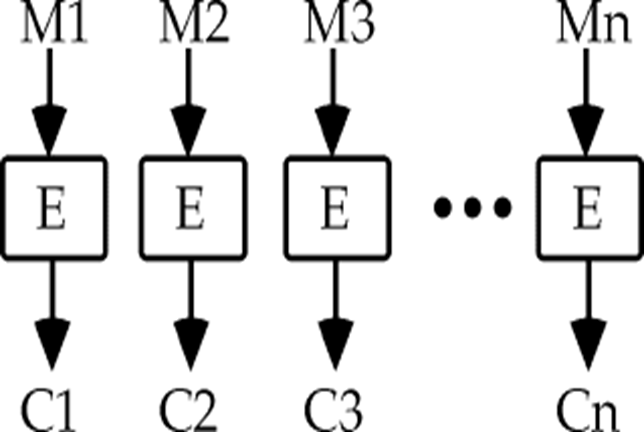
分组密码希望使用对每一块使用尽可能大的替换模块,但并不现实。
当分组长度为64bit时,即需要\(2^{64}\)个实体的替换表,因此使用乘积密码的思想,用一些小的模块替代。
替换-置换密码
Shannon在那篇著名的文章中,介绍了替换-置换(S-P)网络的概念。
- 替换 Substitution
- 置换 Permutation
其实和古典密码的思想类似,替换运算用另一个二进制字代替原来的字。
替换函数就构成密钥,可以看成一个大的查表运算,替换函数也被称为S-box。
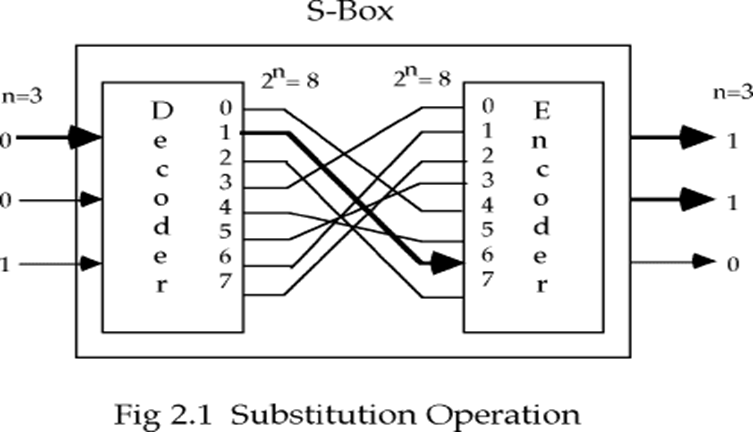
置换运算则打乱一个二进制字的次序,重新排列的方法构成密钥,称为P-box。
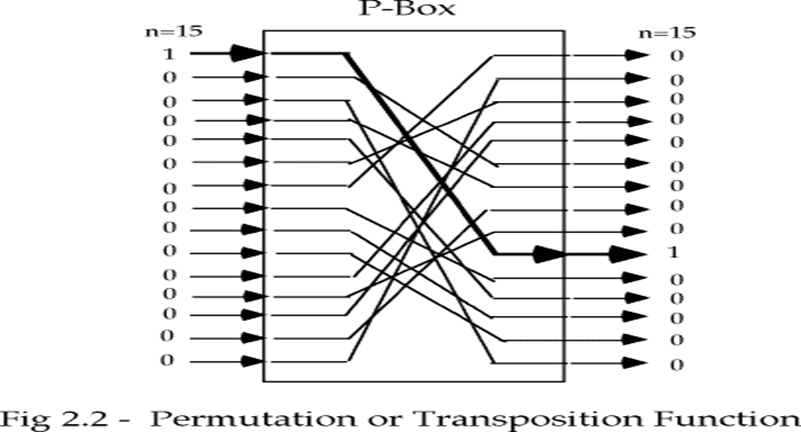
S-P网络就是将这两种运算组合在一起,称为混合变换。
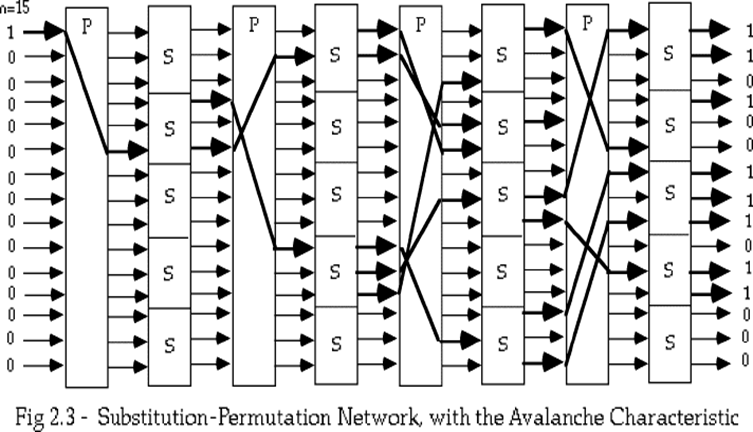
Feistel Cipher
Feitel密码将输入块分为左右两部分L(i-1)和R(i-1),在密码变换的第i轮只使用R(i-1)。
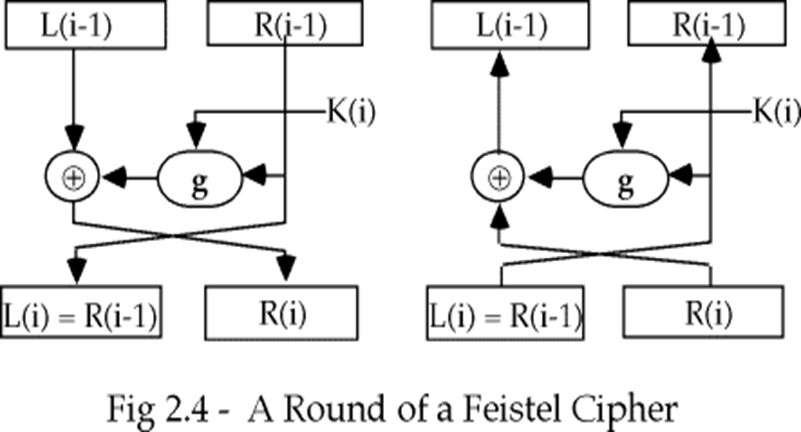
变换过程可以表示为 \[ \begin{align} L(i) &= R(i-1) \\ R(i) &= L(i-1) \oplus g(K(i), R(i-1)) \end{align} \] S盒提供输入bits混合作用(confusion)。
- 使密钥和密文之间关系复杂化
- 极小化统计特性,使统计分析攻击不能奏效。
P盒提供扩散作用(diffusion)
- 将明文和密钥的影响尽可能散步到较多个输出的密文中(将明文冗余度分散到密文中)。
雪崩效应
- 输入改变1bit,导致近半的bit发生变化。
- 对于一个函数\(f\)来说,较好的雪崩特性是指
- 对于\(2^m\)个明文向量,分为\(2^{m-1}\)个向量对\((x_i, x_i')\),每对向量只有一个bit不同。
- 定义\(v_i = f(x) \oplus f(x_i)\),则近半的\(v_i\)为1。
完备性效应
- 每个输出比特是所有输入比特的复杂函数的输出。
- 对于一个函数\(f\)来说,较好的完备性是指
- 对密文输出向量的每一个比特j,至少存在一个明文对\((x_i, x_i')\)。
- 此明文对只在第i比特不同,且\(f(x_i)\)与\(f(x_i')\)的第j比特不同。
Feistel Cipher设计
雪崩特性保证了小的输入变化会导致大的输出变化,完备性保证了每个输出比特依赖于所有的输入比特。
设计密码时需要以下参数
- 分组大小
- 密钥大小
- 轮数
- 子密钥生成
- 轮函数
设计一个快速/安全的算法是困难的。
Lucifer
第一个可用的替换-置换密码。
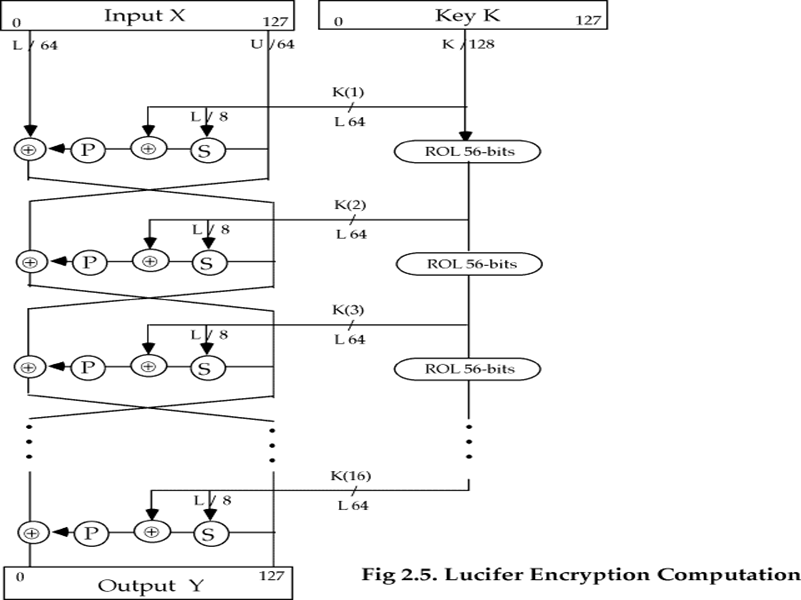
分组长度128bit,密钥长度128bit,每一轮的子密钥是密钥的左半部分。
密钥每次向左旋转56bit,密钥的每部分都参与运算。 \[ \begin{align} L_i &= R_{i-1} \\ R_i &= L_{i-1} \oplus P(K_{i-1}\oplus S(K_{i-1})) \\ K_i &= ROL(K_{i-1}) \end{align} \] Lucifer共有16轮数据计算,使用8对4bitS盒实现替换,用几个8-bit置换组成64bit的简单置换。
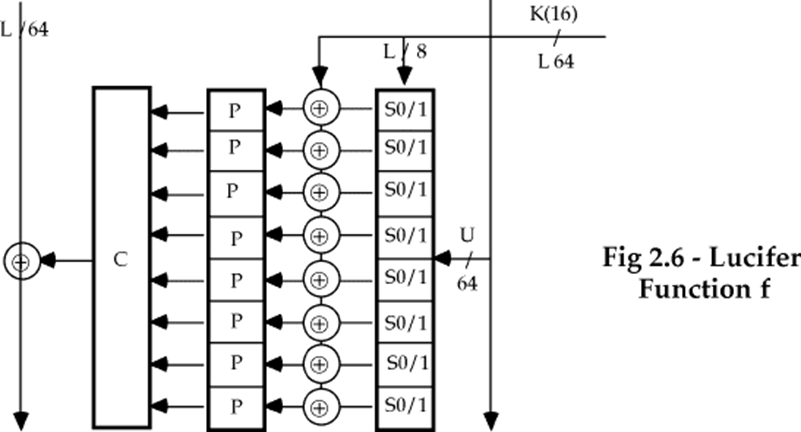
S-DES
S-DES即Simplified DES,供教学使用,有着和DES相似的特性和结构,但参数小。
S-DES主要有以下几个函数
- 初始置换IP(initial permutation)
- 复合函数\(f_k\)$
- 由密钥K确定,具有转换和替换的运算。
- 转换函数SW
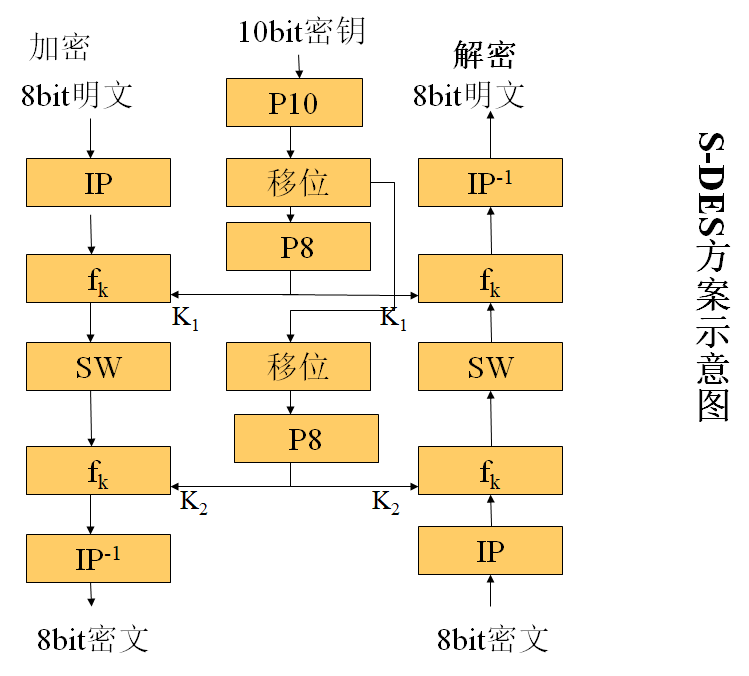
加密算法可以表示为 \[ cipher = IP^{-1}(f_{k2}(SW(f_{k1}(IP(plain))))) \] 其中 \[ K_1 = P_8(移位(P_{10}(K))) \\ K_2 = P_8(移位(移位(P_{10}(K)))) \] 密钥生成可以用下图表示,LS代表循环左移
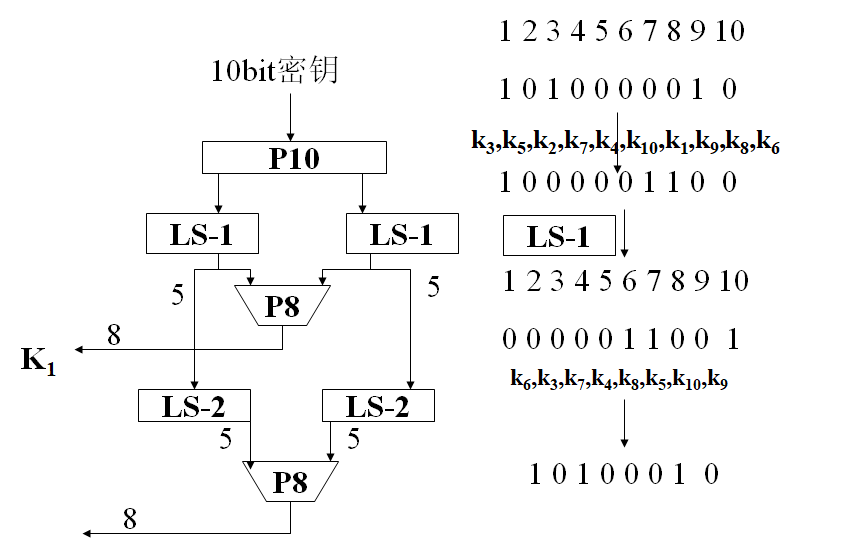
初始置换 \[ IP = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 6 & 3 & 1 & 4 & 8 & 5 & 7 \end{pmatrix} \] \[ IP^{-1} = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 4 & 1 & 3 & 5 & 7 & 2 & 8 & 6 \end{pmatrix} \]
S-DES的加密过程如下
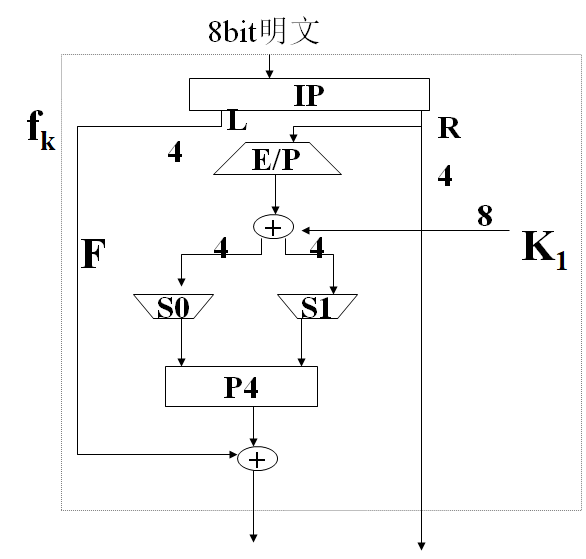
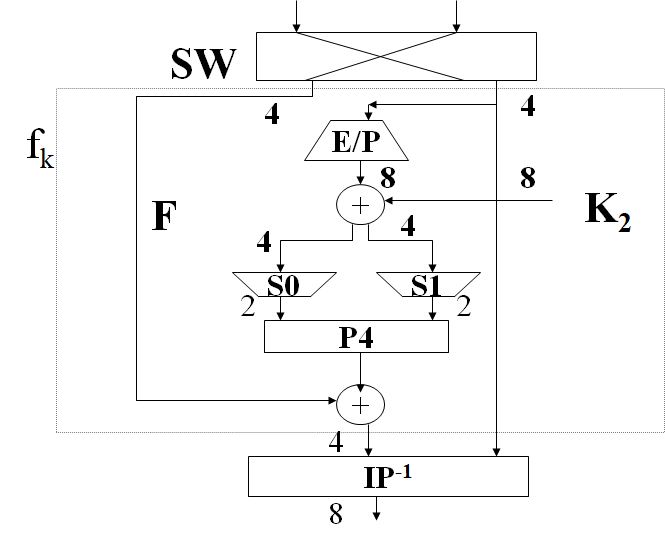
对于S-DES,\(f_k\)是加密方案中最重要的部分 \[ f_k(L, R) = (L\oplus F(R, SK), R) \] 其中对于映射F,输入为4bit,第一步进行扩张/置换(E/P)运算 \[ (n_1, n_2, n_3, n_4) \xrightarrow{E/P} \begin{pmatrix} n_4 & n_1 & n_2 & n_3 \\ n_2 & n_3 & n_4 & n_1 \end{pmatrix} \] 之后将密钥与E/P的结果作异或 \[ \begin{pmatrix} n_4+k_{11} & n_1+k_{12} & n_2+k_{13} & n_3+k_{14} \\ n_2+k_{15} & n_3+j_{16} & n_4+k_{17} & n_1+k_{18} \end{pmatrix} = \begin{pmatrix} P_{0,0} & P_{0,1} & P_{0,2} & P_{0,3} \\ P_{1,0} & P_{1,1} & P_{1,2} & P_{1,3} \end{pmatrix} \] 将第一行和第二行分别输入两个S盒,得到两个2bit的输出。
S盒接收4bit输入,将第1和第4比特组成的数作为行,第2和第3比特组成的数作为列。
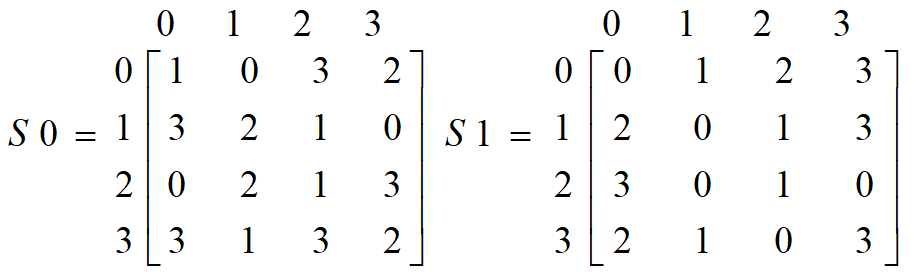
安全分析
对10bit密钥的强行攻击是可行的,可以利用已知明文攻击。
密钥空间:\(2^{10}=1024\)$
已知明文\((p_1, p_2,\dots,p_8)\)和密文\((c_1, c_2,\dots,c_8)\),密钥\((k_1, k_2,\dots,k_{10})\)作为未知数。
S-DES可以表示为8个含10个变量的非线性方程,非线性是S盒作用的结果。
DES
分组长度64bit,密文64bit。密钥为64bit,只有56bit参与运算,8bit作为奇偶校验位。
算法有以下三个阶段
- 对明文X,通过初始置换IP得到\(X_0 = IP(X) = L_0R_0\)$
- 函数F进行16次迭代
- \(L_i = R_{i-1}, R_i = L_{i-1} \oplus F(R_{i-1}, K_i)\quad 1\leq i\leq 16\)$
- \(K_i\)是长为48位的子密钥。
- 对比特串使用逆置换得到密文\(Y=IP^{-1}(R_{16}L_{16})\)$
每一轮的结构可以用下图表示
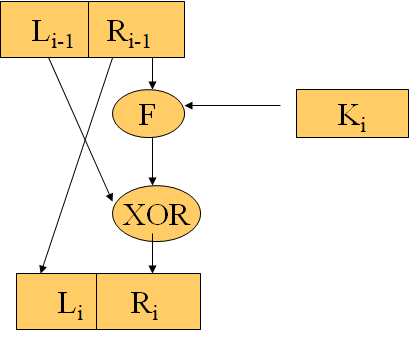
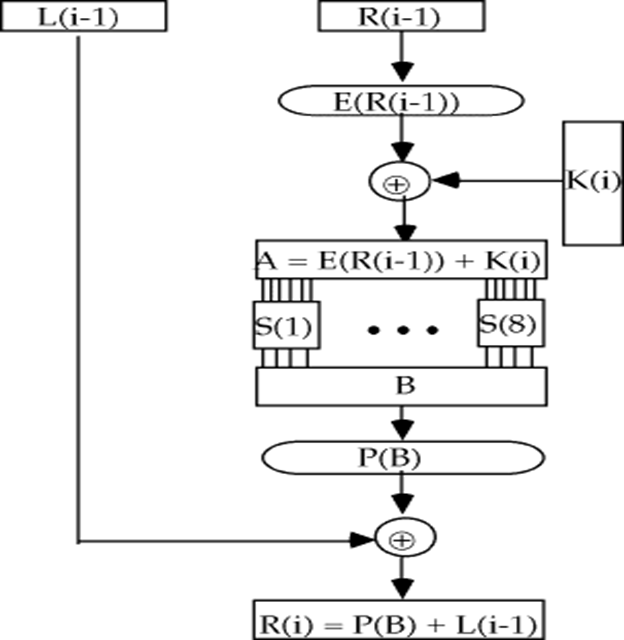
相比于S-DES,DES的F函数更加复杂。
- F的输入为32bit的消息和48bit的密钥,输出为32bit。
- 第一步利用扩展函数,将消息扩展为48bit。
- 随后计算消息与密钥的异或,将48bit写成8个6bit数。
- 用8个S盒接收6bit数的输入,输出8个4bit数。每个S盒是4×16的矩阵,b1b6确定行号,b3b4b5b6确定列号。
- 最后经过一个置换函数得到结果。
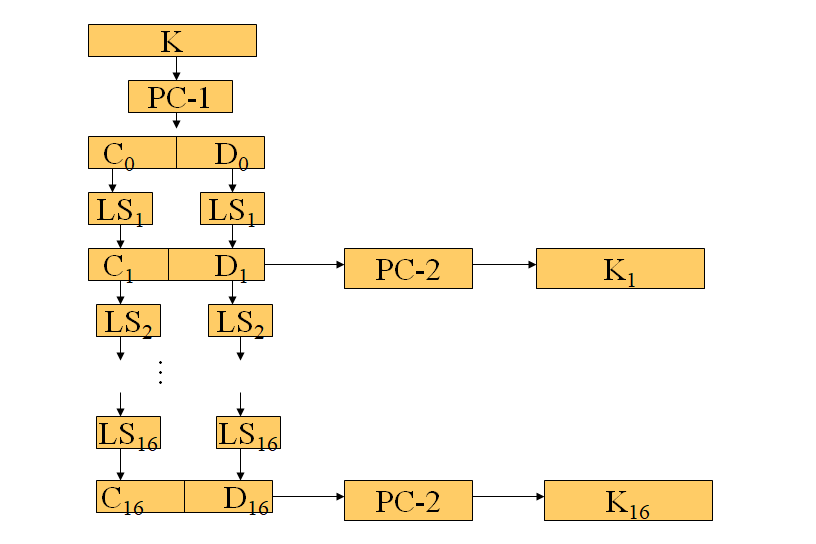
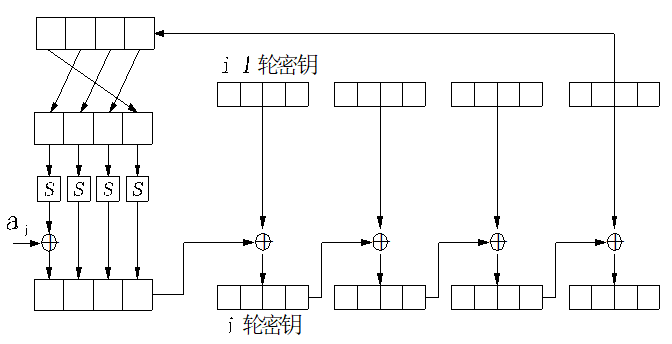
子密钥的生成如下图所示
- PC-1和PC-2都是固定置换,\(LS_i\)表示循环左移。
- 注意\(K_i\)为48bit。
DES的改进
双重DES \[ C = E_{K_2}[E_{K_1}[P]] \\ P = D_{K_1}[D_{K_2}[C]] \] 三重DES \[ C = E_{K_1}[D_{K_2}[E_{K_1}[P]]] \\ P = D_{K_1}[E_{K_2}[D_{K_1}[C]]] \] 三种DES的密钥长度为\(2^{112}\),而标准DES的密钥长度为\(2^{56}\)。
IDEA
分组长度64bit,密钥长度128bit,进行8轮迭代操作。
IDEA中,定义了三种运算。
- 逐位异或
- 整数模\(2^{16}\)加\(\boxplus\)$
- 整数模\(2^{16}+1\)乘\(\boxdot\)(IDEA的S盒)
IDEA的扩散来自于MA结构,它接收两个16bit的明文消息和两个子密钥作为输入,产生两个16bit的输出。
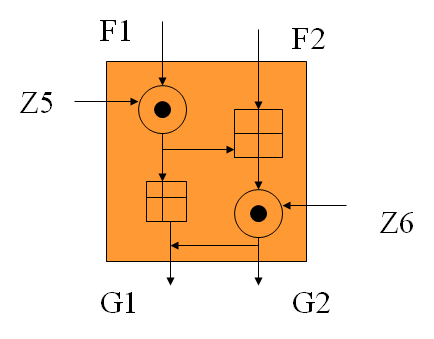
IDEA一共产生52个16bit的子密钥,每一轮使用6个子密钥,另外还需要4个额外子密钥。
前8个子密钥直接从密钥中取出,之后的密钥由25bit的循环左移产生。
- IDEA是PGP的一部分。
- IDEA能抗差分分析和相关分析。
- IDEA似乎没有DES意义下的弱密钥。
AES-Rijndael
分组长度128bit,密钥长度为128、192或256bit,相应的迭代轮数为10、12和14。
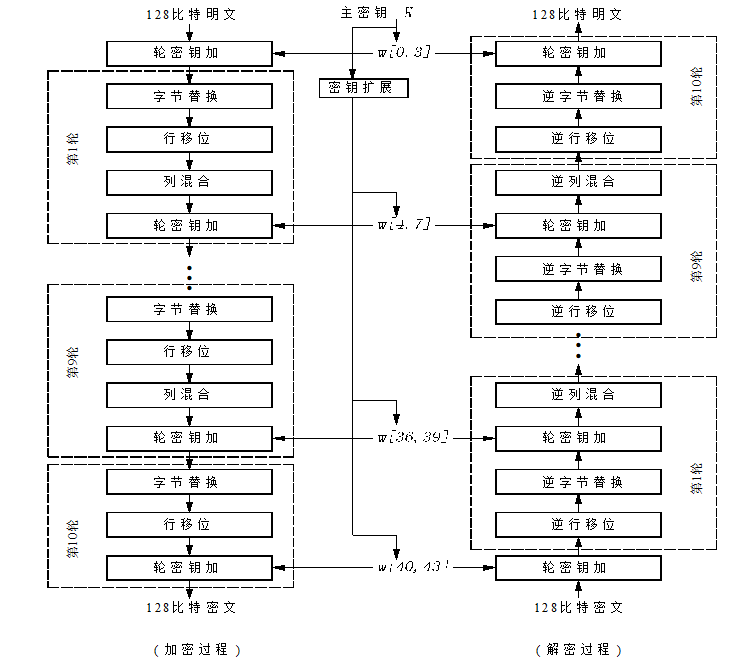
AES的轮函数由四个变换构成,最后一轮省略了列混合。
字节替换
- 替换表是一个16×16的矩阵(S盒)。
- 输入8bit,高4位作为行,低4位作为列,输出8bit。
行移位
- 字节的循环移位运算。
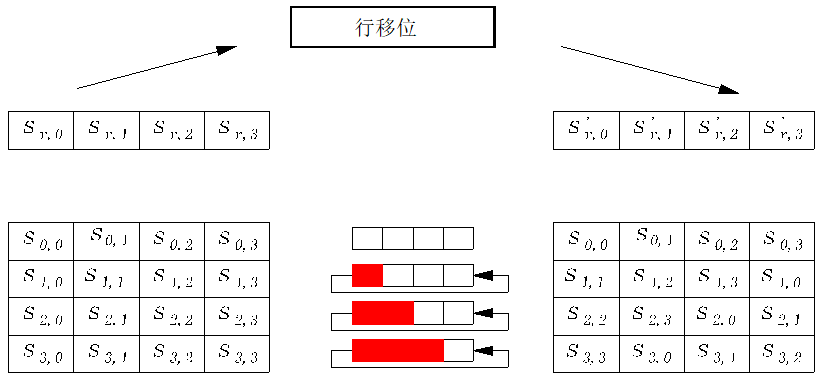
列混合
- 在\(GF(2^8)\)上乘以固定多项式\(a(x)\)并模除\((x^4+1)\)$
- \(S'(x)=a(x)\otimes S(x),\ a(x)=3x^3+x^2+x+2\)$
轮密钥加
- 与每轮的子密钥进行异或操作,子密钥长度等于分组长度。
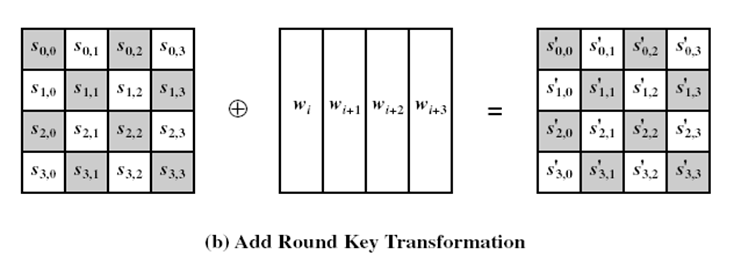
四种变换可以用下图表示
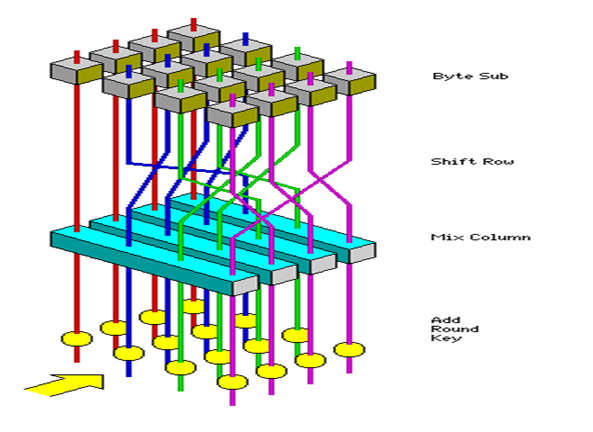
AES的子密钥长度为128bit,也即16个字节,子密钥的生成过程如下。
- 首先将16个字节分为4组,每组4个字节。
- 循环移位后,经过S盒实现替换处理。
- 第一个字节与轮常数异或。
- 将得到的字节与原先的字节按位异或,即为下一轮的密钥。
分组密码的工作模式
DES定义了4种工作模式。
- Block Mode
- ECB
- CBC
- Stream Mode
- CFB
- OFB
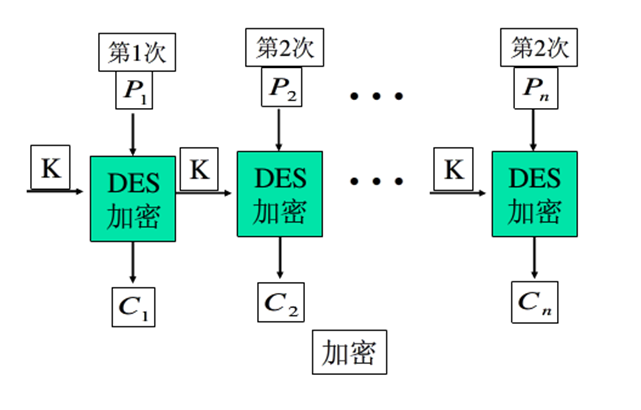
ECB - Electronic Codebook Book
将消息分为独立的加密模块,分组长度为64bit,每块单独使用DES。
适合少量的数据加密,但是对于相同的明文来说,产生的密文也相同(不安全)。
如果需要安全传递DES密钥,ECB是最合适的模式。 \[ C_i = E_K(P_i) \\ P_i = D_K(C_i) \]
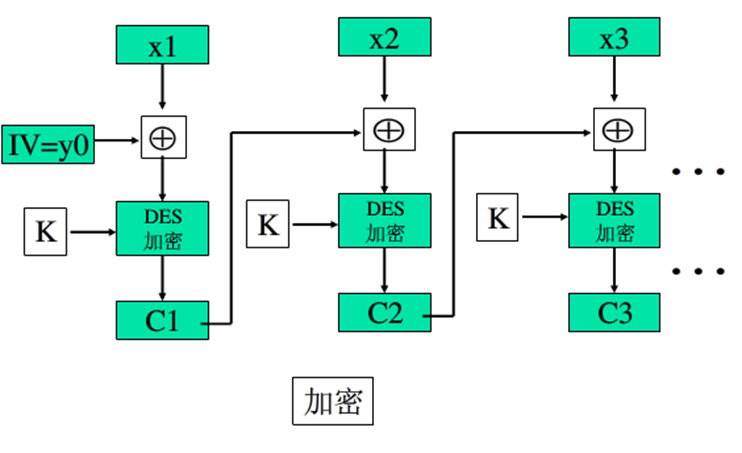
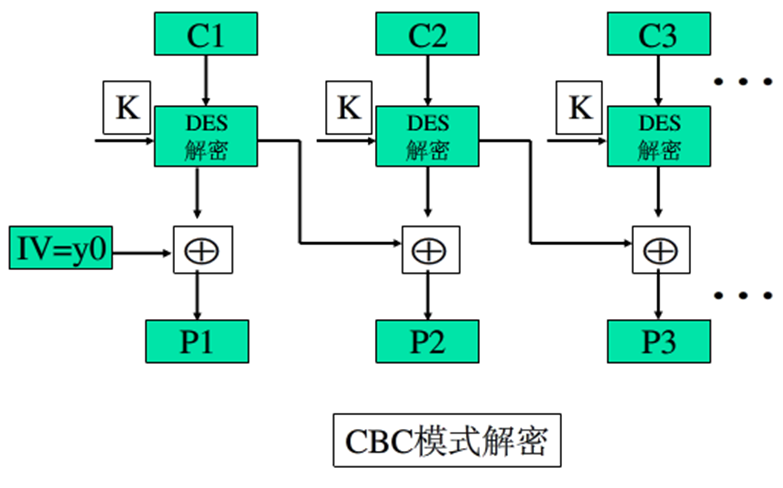
CBC - Cipher Block Chaining
密码分组链接模式构造一个初始向量,将密文与明文联结。
为了提高安全性,应该保护初始向量,可使用ECB加密模式发送。
CBC对于加密长于64bit的消息非常合适,除了能够获得保密性,还可以实现认证(因为初始向量的保密性)。
值得一提的是,如果攻击者能修改IV,则会发生错误传播。 \[
C_i = E_K(C_{i-1}\oplus X_i) \\
X_i = C_{i-1} \oplus D_K(C_i)
\] 

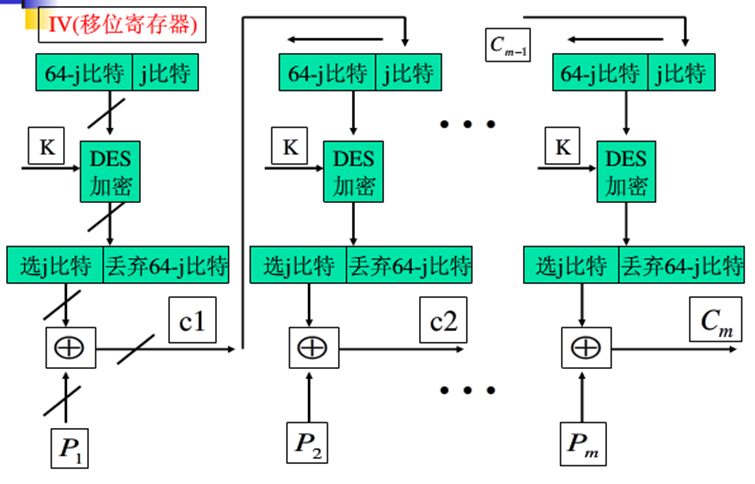
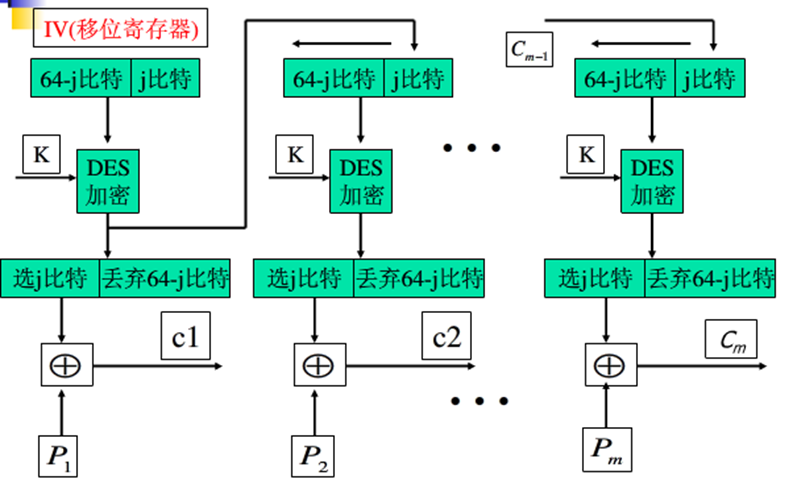
CFB - Cipher FeedBack
DES是分组长为64bit的分组密码,利用CFB模式或OFB模式可以将其转换为流密码。
对于密码反馈模式,加密算法的输入是64bit移位寄存器,初值为一个初始向量。
和CBC模式一样,CFB也可以实现保密与认证,也会发生错误传播。 \[
C_i = P_i \oplus DES_K(C_{i-1}) \\
C_{-1} = IV
\] 
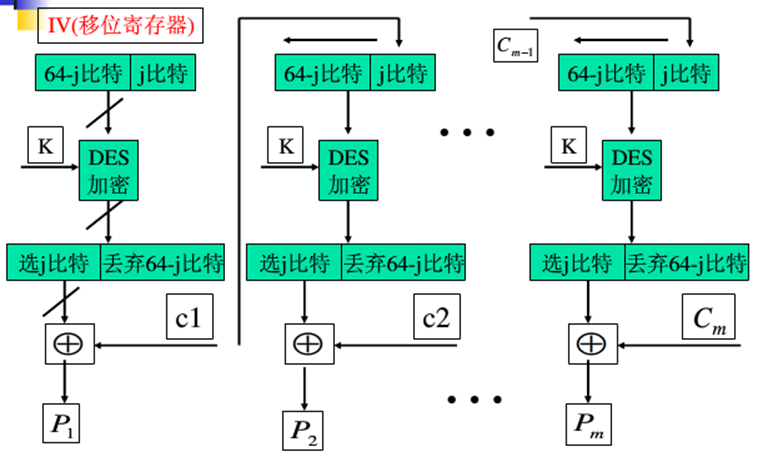
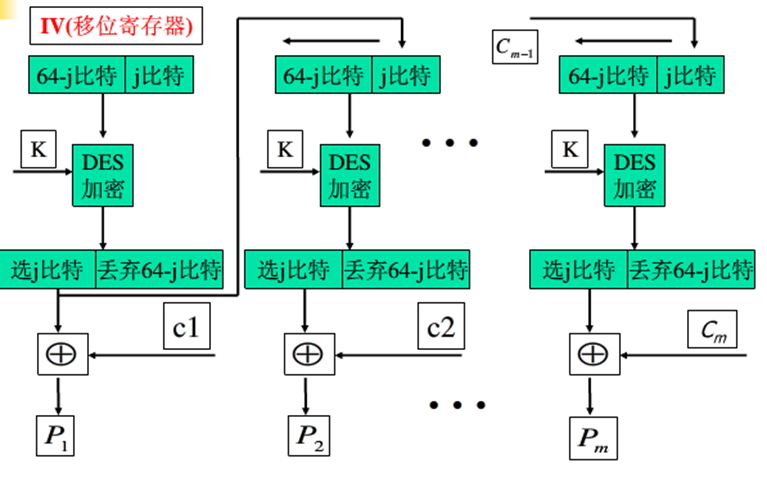
OFB - Output FeedBack
输出反馈方式的结构类似于CFB,不过OFB将加密算法的输出反馈到移位寄存器,而CFB将密文单元反馈到移位寄存器。
OFB的优点是避免了错误传播,如果第一段密文中出错,解密结果中只有第一段明文受影响。
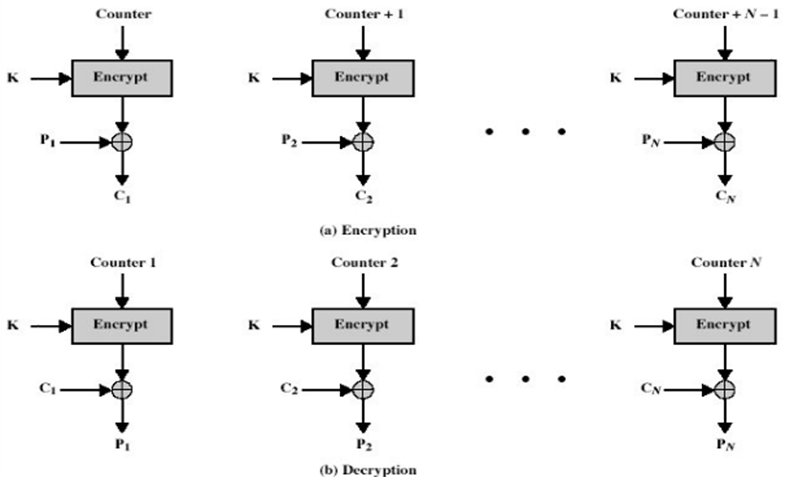
CTR - Counter
计算器模式可以并行加密,并且实现了加密数据块的随机访问。
密码分析攻击
- 唯密文攻击
- 已知明文攻击
- 选择明文攻击
- 自适应选择明文攻击
- 选择密文攻击
- 自适应选择密文攻击
DES可能会受到差分分析攻击(分析明文对的差值对密文对的影响)。