统计学习方法(九)EM算法及其推广
EM算法是一种迭代算法,用于含隐变量的概率模型参数的极大似然估计,或极大后验概率估计。
9.1 EM算法的引入
三硬币模型
假设有三枚硬币,记作A、B、C,这些硬币正面出现的概率分别为π、p、q。进行如下实验:先掷硬币A,根据结果选择硬币,正面选B,反面选C;然后掷选出的硬币,正面记作1,反面记作0;独立重复n次,得到观测结果。
假设只能观测到掷硬币的结果,不能观测过程,问如何估计三硬币正面出现的概率。 \[ \begin{align} P(y|\theta)=\sum_zP(y,z|\theta)&=\sum_zP(z|\theta)P(y|z,\theta) \\ &= \pi p^y(1-p)^{1-y}+(1-\pi)q^y(1-q)^{1-y} \end{align} \] 其中,y表示观测变量,z为隐变量,表示硬币A的结果,θ为模型参数。
将观测数据表示为\(Y=(Y_1,Y_2,\cdots Y_n)^T\),未观测数据表示为\(Z=(Z_1,Z_2,\cdots Z_n)^T\),则似然函数为 \[ \begin{align} P(Y|\theta)&=\sum_ZP(Z|\theta)P(Y|Z,\theta) \\ &= \prod_{j=1}^n[\pi p^{y_i}(1-p)^{1-y_i}+(1-\pi)q^{y_i}(1-q)^{1-y_i}] \end{align} \] 考虑\(\theta=(\pi,p,q)\)的极大似然估计 \[ \hat\theta=\arg\max_\theta\log P(Y|\theta) \]
这个问题没有解析解,只能通过迭代求解,EM算法就是这样一种迭代算法。
EM算法
输入:观测变量数据Y,隐变量数据Z,联合分布\(P(Y,Z|\theta)\),条件分布\(P(Z|Y,\theta)\);
输出:模型参数\(\theta\)。
选择参数的初值\(\theta^{(0)}\),开始迭代;
E步:记\(\theta^{(i)}\)表示第i次迭代时参数的估计值,在第i+1次迭代,计算 \[ \begin{align} Q(\theta,\theta^{(i)})&=E_Z[\log P(Y,Z|\theta)|Y,\theta^{(i)}]\\ &=\sum_Z\log P(Y,Z|\theta)P(Z|Y,\theta^{(i)}) \end{align} \]
M步:求使得\(Q(\theta,\theta^{(i)})\)极大化的参数值,确定第i+1次迭代的参数值 \[ \theta^{(i+1)}=\arg\max_\theta Q(\theta,\theta^{(i)}) \]
重复上述步骤,直到收敛。
参数的初值可以任意选择,但EM算法对初值是敏感的。
停止迭代的条件一般是 \[ \|\theta^{(i+1)}-\theta^{(i)}\|<\epsilon_1 \quad or \quad \|Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})\|<\epsilon_2 \] ### EM算法的导出
面对一个含有隐变量的概率模型,我们希望极大化观测数据关于参数的对数似然函数,即 \[ \begin{align} L(\theta)&=\log P(Y|\theta)=\log\sum_ZP(Y,Z|\theta) \\ &= \log(\sum_ZP(Z|\theta)P(Y|Z,\theta)) \end{align} \] EM算法通过迭代,逐步近似最大化函数,考虑 \[ L(\theta)-L(\theta^{(i)})=\log(\sum_ZP(Z|\theta)P(Y|Z,\theta))-\log P(Y|\theta^{(i)}) \] 利用Jensen不等式 \[ \begin{align} L(\theta)-L(\theta^{(i)})&=\log(\sum_ZP(Z|Y,\theta^{(i)})\frac{P(Z|\theta)P(Y|Z,\theta)}{P(Z|Y,\theta^{(i)})})-\log P(Y|\theta^{(i)})\\ &\geq\sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Z|\theta)P(Y|Z,\theta)}{P(Z|Y,\theta^{(i)})}-\log P(Y|\theta^{(i)})\\ &=\sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Z|\theta)P(Y|Z,\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \end{align} \]
\(\log\sum_j\lambda_jy_j\geq\sum_j\lambda_j\log y_j,\quad\lambda_j\geq0,\quad\sum_j\lambda_j=1\)$
记 \[
B(\theta,\theta^{(i)})\hat=L(\theta^{(i)})+\sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Z|\theta)P(Y|Z,\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})}
\] 则有 \[
L(\theta)\geq B(\theta,\theta^{(i)})
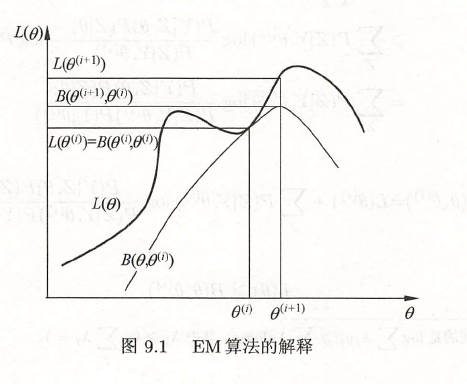
\] 即\(B(\theta,\theta^{(i)})\)是\(L(\theta)\)的一个下界,为了使\(L(\theta)\)尽可能大地增长,选择 \[
\theta^{(i+1)}=\arg\max_\theta B(\theta,\theta^{(i)})
\] 省去常数项,得到 \[
\begin{align}
\theta^{(i+1)}&=\arg\max_\theta(L(\theta^{(i)})+\sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Z|\theta)P(Y|Z,\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})})\\
&=\arg\max_\theta(\sum_ZP(Z|Y,\theta^{(i)})\log P(Z|\theta)P(Y|Z,\theta))\\
&=\arg\max_\theta(\sum_ZP(Z|Y,\theta^{(i)})\log P(Y,Z|\theta))\\
&=\arg\max_\theta Q(\theta,\theta^{(i)})
\end{align}
\] 
9.2 EM算法的收敛性
定理 9.1 设\(P(Y|\theta)\)为观测数据的似然函数,则\(P(Y|\theta^{(i)})\)是单调递增的。
定理 9.2 设\(L(\theta)=\log P(Y|\theta)\)为观测数据的对数似然函数,则有
- 如果\(P(Y|\theta)\)有上界,则\(L(\theta^{(i)}=\log P(Y|\theta^{(i)})\)收敛到某一值。
- 在\(Q(\theta,\theta')\)与\(L(\theta)\)满足一定条件下,由EM算法得到的参数估计序列的收敛值是\(L(\theta)\)的稳定点。
9.3 EM算法在高斯混合模型学习中的应用
高斯混合模型
高斯混合模型是指具有如下形式的概率分布模型 \[ P(y|\theta)=\sum_{k=1}^K\alpha_k\phi(y|\theta_k),\quad\alpha_k\geq0,\quad\sum_{k=1}\alpha_k=1 \] 其中\(\phi(y|\theta_k)\)是高斯分布密度,\(\theta_k=(\mu_k,\sigma_k^2)\),称为第k个分模型。 \[ \phi(y|\theta_k)=\frac1{\sqrt{2\pi}\sigma_k}\exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2}) \]
高斯混合模型参数估计的EM算法
假设观测数据由高斯混合模型生成,我们用EM算法估计高斯混合模型的参数。
明确隐变量,写出对数似然函数
明确隐变量 \[ \gamma_{jk}=\begin{cases}1,\quad第j个观测来自第k个模型\\0,\quad否则\end{cases}\\ j=1,2,\cdots,N;\quad k=1,2,\cdots,K \] 写出似然函数 \[ \begin{align} P(y,\gamma|\theta)&=\prod_{j=1}^NP(y_j,\gamma_{j1},\gamma_{j2},\cdots,\gamma_{jK}|\theta)\\ &=\prod_{k=1}^K\prod_{j=1}^N[\alpha_k\phi(y_j|\theta_k)]^{\gamma_{jk}}\\ &=\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N[\phi(y_j|\theta_k)]^{\gamma_{jk}}\\ &=\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N[\frac1{\sqrt{2\pi}\sigma_k}\exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2}]^{\gamma_{jk}} \end{align} \] 其中,\(n_k=\sum_{j=1}^N\gamma_{jk}\),\(\sum_{k=1}^Kn_k=N\)$
那么对数似然函数为 \[ \log P(y,\gamma|\theta)=\sum_{k=1}^K\{n_k\log\alpha_k+\sum_{j=1}^N\gamma_{jk}[\log(\frac1{\sqrt{2\pi}})-\log\sigma_k-\frac1{2\sigma_k^2}(y-\mu_k)^2]\} \]
EM算法的E步:确定Q函数
\[ \begin{align} Q(\theta,\theta^{(i)})&=E[\log P(y,\gamma|\theta)|y,\theta^{(i)}]\\ &=E\{\sum_{k=1}^K\{n_k\log\alpha_k+\sum_{j=1}^N\gamma_{jk}[\log(\frac1{\sqrt{2\pi}})-\log\sigma_k-\frac1{2\sigma_k^2}(y-\mu_k)^2]\}\}\\ &=\sum_{k=1}^K\{\sum_{j=1}^N(E\gamma_{jk})\log\alpha_k+\sum_{j=1}^N(E\gamma_{jk})[\log(\frac1{\sqrt{2\pi}})-\log\sigma_k-\frac1{2\sigma_k^2}(y-\mu_k)^2]\} \end{align} \]
这里需要计算\(E(\gamma_{jk}|y,\theta)\)$
\[ \begin{align} \hat\gamma_{jk}&=E(\gamma_{jk}|y,\theta)=P(\gamma_{jk}=1|y,\theta)\\ &=\frac{P(\gamma_{jk}=1,y_j|\theta)}{\sum_{k=1}^KP(\gamma_{jk}=1,y_j|\theta)}\\ &=\frac{P(y_j|\gamma_{jk}=1,\theta)P(\gamma_{jk}=1|\theta)}{\sum_{k=1}^KP(y_j|\gamma_{jk}=1,\theta)P(\gamma_{jk}=1|\theta)}\\ &=\frac{\alpha_k\phi(y_j|\theta_k)}{\sum_{k=1}^K\alpha_k\phi(y_j|\theta_k)},\quad j=1,2,\cdots,N;\quad k=1,2,\cdots,N \end{align} \]
代回原式 \[ Q(\theta,\theta^{(i)})=\sum_{k=1}^K\{n_k\log\alpha_k+\sum_{j=1}^N\hat\gamma_{jk}[\log(\frac1{\sqrt{2\pi}})-\log\sigma_k-\frac1{2\sigma_k^2}(y-\mu_k)^2]\} \]
确定EM算法的M步
\[ \theta^{(i+1)}=\arg\max_\theta Q(\theta,\theta^{(i)}) \]
将\(Q(\theta,\theta^{(i)})\)分别对\(\mu_k,\sigma_k^2\)求偏导数,令其为0;求\(\hat\alpha_k\)是在\(\sum_{k=1}^K\alpha_k=1\)条件下求偏导数并令其为0得到的。
\[ \hat\mu_k=\frac{\sum_{j=1}^N\hat\gamma_{jk}y_j}{\sum_{j=1}^N\hat\gamma_{jk}},\quad k=1,2,\cdots,K\\ \hat\sigma_k^2=\frac{\sum_{j=1}^N\hat\gamma_{jk}(y_j-\mu_k)^2}{\sum_{j=1}^N\hat\gamma_{jk}},\quad k=1,2,\cdots,K\\ \hat\alpha_k=\frac{n_k}N=\frac{\sum_{j=1}^N\hat\gamma_{jk}}{N},\quad k=1,2,\cdots,K\\ \]
9.4 EM算法的推广
暂略,有空再补。
F函数的极大-极大算法
GEM算法
Scikit-learn
from sklearn.mixture import GaussianMixture
import numpy as np
import matplotlib.pyplot as plt
# 初始化观测数据
data = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28, 29, 41, 49, 56, 60,
75]).reshape(-1, 1)
# 聚类
gmmModel = GaussianMixture(n_components=2)
gmmModel.fit(data)
labels = gmmModel.predict(data)
print("labels =", labels)总结
对于含隐变量的模型,分E步和M步,分别求期望和极大值,得到参数的新的估计值,迭代以极大化函数。