统计学习方法(六)Logistic回归与最大熵模型
Logistic回归是统计学习中的分类方法,最大熵是概率模型学习的一个准则,推广到分类问题得到最大熵模型。
6.1 Logistic回归模型
Logistic分布
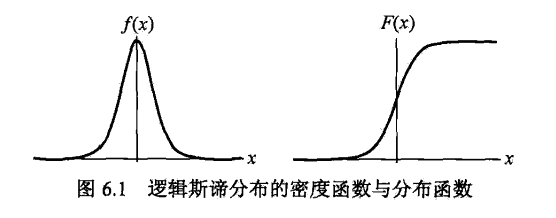
设X为连续随机变量,X服从Logistic分布是指 \[ F(x) = P(X\leq x) = \frac 1 {1+e^{-(x-\mu)/\gamma}} \\ f(x) = F'(x) = \frac {e^{-(x-\mu)/\gamma}} {\gamma(1+e^{-(x-\mu)/\gamma})^2} \] 其中\(\mu\)为位置参数,\(\gamma > 0\)为形状参数
分布函数的图形是S形曲线,关于点\((\mu, \frac 1 2)\)中心对称 \[
F(\mu-x) + F(x-\mu) = 1
\] 
二项Logistic回归模型
二项Logistic回归模型是一种分类模型,由条件概率\(P(Y|X)\)表示,其中随机变量Y取值为1或0,条件概率分布如下: \[ P(Y=1|x) = \frac {\exp(w\cdot x+b)} {1 + \exp(w\cdot x+b)} \\ P(Y=0|x) = \frac {1} {1 + \exp(w\cdot x+b)} \] w称为权值向量,b称为偏置。
有时为了方便,用如下记法 \[ P(Y=1|x) = \frac {\exp(w\cdot x)} {1 + \exp(w\cdot x)} \\ P(Y=0|x) = \frac {1} {1 + \exp(w\cdot x)} \\ w = (w^{(1)}, w^{(2)},\cdots, w^{(n)}, b) ,\quad x = (x^{(1)}, x^{(2)}, \cdots, x^{(n)}, 1) \] 注意到 \[ \log\frac{P(Y=1|x)}{1 - P(Y=1|x)} = w\cdot x \] 输出Y=1的对数几率是输入x的线性函数表示的模型,即Logistic模型。
模型参数估计
对于给定的训练集T,可以用极大似然估计法估计模型参数。 \[ P(Y=1|x) = \pi(x),\quad P(Y=0|x) = 1-\pi(x) \] 似然函数为 \[ \prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} \] 对数似然函数为 \[ \begin{align} L(w) &= \sum_{i=1}^N[y_i\log\pi(x_i)+(1-y_i)log(1-\pi(x_i))] \\ &= \sum_{i=1}^N[y_i\log\frac{\pi(x_i)}{1-\pi(x_i)}+log(1-\pi(x_i))] \\ &= \sum_{i=1}^N[y_i(w\cdot x_i)-log(1+\exp(w\cdot x_i))] \end{align} \] 对L(w)求极大值,得到w的估计值。
这样问题就变成了以L(w)为目标函数的最优化问题,通常采用梯度下降法及拟牛顿法。
多项Logistic回归
上述的模型是二分类模型,可以推广为多分类模型。
假设Y的取值集合是\(\{1,2,\cdots,K\}\),则多项Logistic模型为 \[ P(Y=k|x) = \frac {\exp(w_k\cdot x+b)} {1 + \sum_k\exp(w_k\cdot x+b)} \\ P(Y=K|x) = \frac 1 {1 + \sum_k\exp(w_k\cdot x+b)} \\ k = 1,2, \cdots, K-1 \]
6.2 最大熵模型
最大熵原理
假设离散随机变量X的概率分布是P(X),则熵为 \[ H(P) = -\sum_xP(x)\log P(x) \] 熵满足下列不等式 \[ 0 \leq H(P) \leq \log |X| \] 当且仅当X服从均匀分布时,熵最大。
模型定义
假设分类模型是条件概率分布,给定训练集T,学习的目标是用最大熵原理选择最好的分类模型。
训练集的经验分布 \[ \widetilde P(X=x, Y=y) = \frac {\nu(X=x,Y=y)}{N}\\ \widetilde P(X=x) = \frac {\nu(X=x)}{N} \] 其中\(\nu(X=x,Y=y)\)表示样本出现的频数。
用特征函数描述输入与输出的关系 \[ f(x,y) = \begin{cases} 1, \quad x与y满足某一事实 \\ 0, \quad否则\end{cases} \] 经验分布 \[ E_{\widetilde{P}}(f) = \sum_{x,y}\widetilde P(x,y)f(x,y) \\ E_{\widetilde{P}}(f) = \sum_{x,y}\widetilde P(x)P(y|x)f(x,y) \] 如果模型能够获取训练集中的数据,即可认为两个期望值相等。
假设满足所有约束条件的模型集合为 \[ {\cal C} = \{P\in {\cal P}|E_P(f_i) = E_{\widetilde P}(f_i), \quad i=1,2,\cdots,n\} \] 定义在条件概率分布P(Y|X)熵的条件熵为 \[ H(P) = -\sum_{x,y}\widetilde P(x)P(y|x)\log P(y|x) \] 则模型集合中条件熵最大的模型称为最大熵模型。
模型学习
给定训练集以及特征函数,最大熵模型的学习等价于约束最优化问题 \[ \begin{align} \min_{\cal P\in C}&& &-H(P) = \sum_{x,y}\widetilde P(x)P(y|x)\log P(y|x) \\ s.t.&& &E_P(f_i) - E_{\widetilde P}(f_i)=0,\quad i=1,2,\cdots,n \\ && &\sum_yP(y|x) = 1 \\ \end{align} \] 将约束最优化的原始问题转化为无约束最优化的对偶问题,通过拉格朗日乘数法求解。
引入拉格朗日乘子,定义拉格朗日函数 \[ \begin{align} L(P,w) &= -H(P) + w_o(1-\sum_yP(y|x))+\sum_{i=1}^nw_i(E_P(f_i) - E_{\widetilde P}(f_i)) \\ &= \sum_{x,y}\widetilde P(x)P(y|x)\log P(y|x) + w_o(1-\sum_yP(y|x)) \\ &\quad +\sum_{i=1}^nw_i(\sum_{x,y}\widetilde P(x,y)f_i(x,y) - \sum_{x,y}\widetilde P(x)P(y|x)f_i(x,y)) \end{align} \] 原始问题是 \[ \min_{\cal P\in C}\max_wL(P,w) \] 对偶问题是 \[ \max_{w}\min_{\cal P\in C}L(P,w) \]
具体地 \[ \begin{align} \frac {\part L(P,w)} {\part P(y|x)} &= \sum_{x,y}\widetilde P(x)(logP(y|x)+1)-\sum_yw_0-\sum_{x,y}(\widetilde P(x)\sum_{i=1}^nw_if_i(x,y)) \\ &= \sum_{x,y}\widetilde P(x)(logP(y|x)+1-w_0-\sum_{i=1}^nw_if_i(x,y)) \end{align} \] 令\(\frac {\part L(P,w)} {\part P(y|x)}=0\),得到 \[ P_w(y|x) = \frac 1 {Z_w(x)}\exp(\sum_{i=1}^nw_if_i(x,y)) \\ Z_w(x) = \sum_y\exp(\sum_{i=1}^nw_if_i(x,y)) \] \(Z_w(x)\)称为规范化因子,\(f_i(x,y)\)是特征函数,由此表示的模型\(P_w\)就是最大熵模型。
对偶函数的极大化,等价于最大熵模型的极大似然估计。
6.3 模型学习的最优化算法
改进的迭代尺度法
改进的迭代尺度法(improved iterative scaling,IIS)基本想法是,找到新的参数向量\(w+\delta\),使得模型的对数似然函数值增大,即 \[ \begin{align} L(w+\delta) - L(w) &= \sum_{x,y}\widetilde P(x,y)\log P_{w+\delta}(y|x) - \widetilde P(x,y)\log P_{w}(y|x) \\ &= \sum_{x,y}\widetilde P(x,y)\sum_{i=1}^n\delta_if_i(x,y) - \sum_x\widetilde P(x)\log \frac{Z_{w+\delta}(x)}{Z_w(x)} \geq 0 \end{align} \] 利用不等式 \[ -\log\alpha\geq1-\alpha,\quad\alpha>0 \] 由此 \[ \begin{align} L(w+\delta) - L(w) &\geq \sum_{x,y}\widetilde P(x,y)\sum_{i=1}^n\delta_if_i(x,y)+1-\sum_x\widetilde P(x)\frac{Z_{w+\delta}(x)}{Z_w(x)} \\ &= \sum_{x,y}\widetilde P(x,y)\sum_{i=1}^n\delta_if_i(x,y)+1-\sum_x\widetilde P(x)\sum_yP_w(y|x)\exp\sum_{i=1}^n\delta_if_i(x,y) \\ &= A(\delta|w) \end{align} \] 即\(A(\delta|w)\)是改变量的一个下界,IIS试图每次只优化其中一个变量\(\delta_i\),而固定其他变量。
通过推算,可以得到新的(相对不紧的)下界 \[ L(w+\delta)-L(w)\geq B(\delta|w) \] 通过对\(B(\delta|w)\)求偏导数,并令其为0,得到相应的等式,依次求解方程即可。
算法
输入:特征函数,经验分布,模型
输出:最优参数值,最优模型
步骤:
\(\forall i\in\{1,2,\cdots,n\},\quad w_i=0\)$
\(\forall i\in\{1,2,\cdots,n\}\)$
\(\delta_i\)满足方程 \[ \sum_{x,y}\widetilde P(x)P(y|x)f_i(x,y)\exp(\delta_if^\#(x,y)) = E_{\widetilde P}(f_i) \] 其中 \[ f^\#(x,y) = \sum_{i=1}^nf_i(x,y) \]
更新\(w_i\):\(w_i\leftarrow w_i+\delta_i\)$
重复直至所有\(w_i\)都收敛
拟牛顿法
略。
Scikit-learn
from sklearn.linear_model import LogisticRegression
# solver: liblinear, lbfgs, newton-cg, sag
clf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
print(clf.coef_, clf.intercept_)