统计学习方法(五)决策树
决策树是一种基本的分类与回归方法,在分类问题中,用树形结构表示基于特征对实例进行分类的过程。
5.1 决策树模型与学习
定义
决策树是一种描述对实例进行分类的树形结构,由节点和有向边组成。
节点有两种类型:内部节点和叶子节点,内部节点表示特征或属性,叶子结点表示一个类。
决策树分类时,从根节点开始,对实例的某一特征进行测试,根据测试结果将其分配到子节点。如此递归,直至到达叶节点,最后分到叶节点的类中。
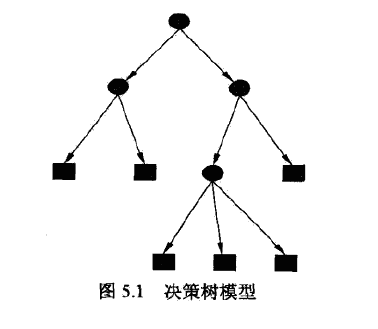
决策树学习
可以把决策树看成if-then规则的集合,每个实例只被一条路径或一条规则所覆盖。
也可以从条件概率分布的角度理解,定义在特征空间的划分上,将特征空间分为互不相交的单元或区域,在每个单元上定义一个类的概率分布就构成了一个条件概率分布。
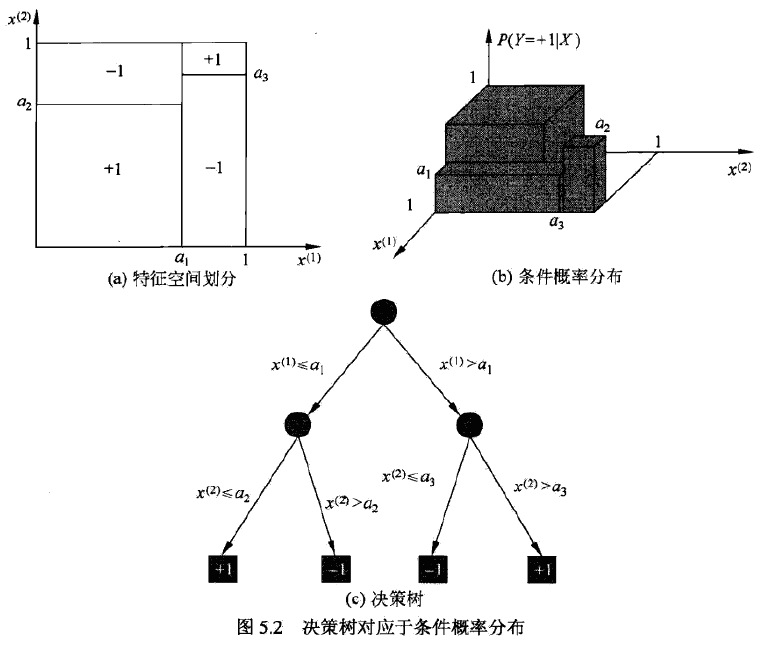
决策树学习在本质上,是从训练集中归纳出一组分类规则,我们需要的是一个与训练集矛盾较小的决策树,同时具有很好的泛化能力。
决策树的损失函数通常是正则化的极大似然函数,学习策略是最小化损失函数。
5.2 特征选择
特征选择,是决定用哪个特征来划分特征空间。
信息增益
首先给出熵与条件熵的定义 \[ H(X)=-\sum_{i=1}^np_i\log p_i \\ 0 \leq H(p) \leq \log n \] 熵越大,随机变量的不确定性就越大。 \[ H(Y|X) = \sum_{i=1}^nP(X=x_i)H(Y|X=x_i) \] 当熵和条件熵中的概率由数据估计得到时,称为经验熵与经验条件熵。
信息增益,定义为集合D的经验熵与特征A给定条件D下的经验条件熵之差 \[ g(D,A) = H(D) - H(D|A) \]
一般,熵与条件熵之差称为互信息,信息增益等价于训练集中类与特征的互信息。
对于训练数据集D,计算每个特征的信息增益,比较大小,选择信息增益最大的特征。
信息增益比
\[ g_k(D,A) = \frac {g(D,A)} {H(D)} \]
5.3 决策树的生成
ID3算法
ID3算法,核心是在决策树每个节点上应用信息增益准则选择特征,递归地构建决策树。
输入:训练数据集D,特征集A,阈值ε
输出:决策树T
若D中所有实例属于同一类\(C_k\),则T为单节点树,返回T;
若A为空集,则返回T;
否则,计算A中各特征对D的信息增益,选择信息增益最大的特征\(A_g\);
若\(A_g\)的信息增益小于阈值,则返回T;
否则,对\(A_g\)的每一可能值,以此将D分割成若干非空子集,将实例树最大的类作为标记,构建子节点,由节点及其子节点构成树T,返回T;
对第i个子节点,以\(D_i\)为训练集,\(A-{A_g}\)为特征集,递归调用上述步骤,得到子树\(T_i\),返回\(T_i\)。
ID3算法只有树的生成,容易产生过拟合。
C4.5算法
改进处在于,用信息增益比来选择特征。
5.4 决策树的剪枝
剪枝是为了解决过拟合现象,对已生成的决策树进行简化。
剪枝往往通过极小化损失函数或代价函数来实现。
设树T的叶子结点个数为|T|,t为T的叶子结点,t有\(N_t\)个样本点,其中k类的样本点有\(N_{tk}\)个,\(H_t(T)\)为t的经验熵,则损失函数可以定义为 \[ C_\alpha(T) = \sum_{t=1}^{|T|}N_tH_t(T)+\alpha|T| \\ H_t(T) = -\sum_k\frac{N_{tk}}{N_t}\log\frac{N_{tk}}{N_t} \] 记 \[ C(T) = \sum_{t=1}^{|T|}N_tH_t(T) = -\sum_{t=1}^{|T|}\sum_{k=1}^KN_{tk}\log\frac{N_{tk}}{N_t} \] 则有 \[ C_\alpha(T) = C(T) + \alpha|T| \] 剪枝算法
输入:生成算法产生的整个树T,参数α
输出:修剪后的子树\(T_\alpha\)$
- 计算每个节点的经验熵
- 递归地从树的叶子结点向上回溯
- 设叶节点回溯到父节点之前与之后的树分别为\(T_B\)与\(T_A\),如果\(C_\alpha(T_A)\leq C_\alpha(T_B)\),则进行剪枝,将父节点变为新的叶子结点。
- 直至不能继续为止,得到损失函数最小的子树
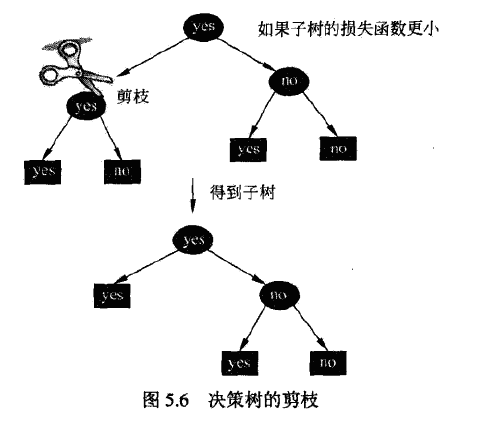
5.5 CART算法
CART同样由特征选择、树的生成及剪枝组成,既可以用于分类也可以用于回归。
CART生成
回归树
X与Y为输入和输出变量,Y是连续变量,给定训练集 \[ D = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} \] 假设已将输入空间划分为M个单元\(R_1,R_2,...,R_M\),并且在每个单元\(R_m\)上有一个固定的输出值\(c_m\),那么回归树模型可表示为 \[ f(x) = \sum_{m=1}^Mc_mI(x\in R_m) \] 当输入空间的划分确定时,可以用平方误差来表示回归树的预测误差 \[ \sum_{x_i\in R_m}(y_i-f(x_i))^2 \\ \hat c_m = {\rm ave} (y_i|x_i\in R_m) \] 采用启发式的方法对输入空间进行划分,选择第j个变量\(x^{(j)}\)和取值s,作为切分变量和切分点,并定义两个区域: \[ R_1(j,s) = \{x|x^{(j)}\leq s\} \quad R_2(j,s) = \{x|x^{(j)}> s\} \] 由此找到最优切分点s \[ \hat c_1 = {\rm ave} (y_i|x_i\in R_1(j,s)) \quad \hat c_2 = {\rm ave} (y_i|x_i\in R_2(j,s)) \] 遍历所有变量,找到最优的切分变量j,以此划分输入空间,然后对每个区域重复上述过程,知道满足条件,由此生成一棵回归树,通常称为最小二乘回归树。
分类树
分类树用基尼指数选择最优特征,同时决定该特征的最优二值切分点。
分类问题中,假如有K个类,样本点属于第k类的概率为\(p_k\),则基尼指数定义为 \[ Gini(p) = \sum_{k=1}^Kp_k(1-p_k) = 1 - \sum_{k=1}^Kp_k^2 \] K=2时 \[ Gini(p) = 2p(1-p) \] 如果样本集合D根据特征A是否取可能值进行分割,即 \[ D_1 = \{(x,y)\in D|A(x)=a\}, \quad D_2 = D - D_1 \] 在特征A的条件下,基尼指数定义为 \[ Gini(D,A) = \frac {|D_1|} {D} Gini(D_1)+\frac {|D_2|} {D} Gini(D_2) \] 基尼指数表示集合D的不确定性,基尼指数越大,样本集合的不确定性越大。
在分类树中,选择基尼指数最小的特征作为最优特征。
CART剪枝
输入:CART生成的决策树\(T_0\)$
输出:最优决策树\(T_\alpha\)$
设\(k=0,T=T_0\)$
设\(\alpha=+\infty\)$
自下而上地对各内部节点计算\(C(T_t),|T_t|\)以及 \[ g(t) = \frac {C(t) - C(T_t)} {|T_t|-1} \]
\[ \alpha = min(\alpha, g(t)) \]
自上而下地访问内部节点,如果\(g(t) = \alpha\),进行剪枝,并以多数表决法决定其类,得到T
设\(k=k+1,\alpha_k=\alpha,T_k=T\)$
如果T不是由根节点单独构成的树,回到第四步
采用交叉验证法,在子树序列中选取最优子树
Scikit-learn
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)
clf.score(X_test, y_test)
tree_pic = export_graphviz(clf, out_file="mytree.pdf")
with open('mytree.pdf') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)总结
总体思路就是构造决策树,根据损失函数进行剪枝,具体细节没怎么看懂,回头找份代码瞧瞧。